NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.1
Page No: 99
Ex 5.1 Class 10 Maths Question 1.
In which of the following situations, does the list of numbers involved make an arithmetic progression and why?
(i) The taxi fare after each km when the fare is ₹ 15 for the first km and ₹ 8 for each additional km.
(ii) The amount of air present in a cylinder when a vacuum pump removes (frac { 1 }{ 4 }) of the air remaining in the cylinder at a time.
(iii) The cost of digging a well after every meter of digging, when it costs ₹ 150 for the first meter and rises by ₹ 50 for each subsequent meter.
(iv) The amount of money in the account every year, when ₹ 10000 is deposited at compound interest at 8% per annum.
Solution:


Ex 5.1 Class 10 Maths Question 2.
Write first four terms of the AP, when the first term a and the common difference d are given as follows:
(i) a = 10, d = 10
(ii) a = -2, d = 0
(iii) a = 4, d = -3
(iv) a = -1, d = (frac { 1 }{ 2 })
(v) a = -1.25, d = -0.25
Solution:


You can also download the free PDF of Ex 5.1 Class 10 Arithmetic Progressions NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.
Download NCERT Solutions For Class 10 Maths Chapter 5 Arithmetic Progressions PDF
Ex 5.1 Class 10 Maths Question 3.
For the following APs, write the first term and the common difference:
(i) 3, 1, -1, -3, ……
(ii) -5, -1, 3, 7, ……
(iii) (frac { 1 }{ 3 }) , (frac { 5 }{ 3 }) , (frac { 9 }{ 3 }), (frac { 13 }{ 3 }) , ……..
(iv) 0.6, 1.7, 2.8, 3.9, …….
Solution:
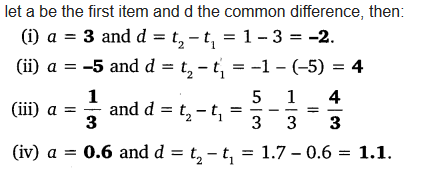
Ex 5.1 Class 10 Maths Question 4.
Which of the following are APs ? If they form an AP, find the common difference d and write three more terms.
(i) 2, 4, 8, 16, …….
(ii) 2, (frac { 5 }{ 2 }) , 3, (frac { 7 }{ 2 }) , …….
(iii) -1.2, -3.2, -5.2, -7.2, ……
(iv) -10, -6, -2,2, …..
(v) 3, 3 + (sqrt { 2 } ), 3 + 2(sqrt { 2 } ), 3 + 3(sqrt { 2 } ), …..
(vi) 0.2, 0.22, 0.222, 0.2222, ……
(vii) 0, -4, -8, -12, …..
(viii) (frac { -1 }{ 2 }) , (frac { -1 }{ 2 }) , (frac { -1 }{ 2 }) , (frac { -1 }{ 2 }) , …….
(ix) 1, 3, 9, 27, …….
(x) a, 2a, 3a, 4a, …….
(xi) a, a2, a3, a4, …….
(xii) (sqrt { 2 } ), (sqrt { 8 } ), (sqrt { 18 } ), (sqrt { 32 } ), …..
(xiii) (sqrt { 3 } ), (sqrt { 6 } ), (sqrt { 9 } ), (sqrt { 12 } ), …..
(xiv) 12, 32, 52, 72, ……
(xv) 12, 52, 72, 73, ……
Solution:



Class 10 Maths Arithmetic Progressions Mind Maps
Arithmetic Progression (AP)
Consider
(i) 1, 2, 3, 4, ……
(ii) 3, 3, 3, 3, …..
(i) and (ii) are the sequence of numbers, each number in these sequences is called a term.
An arithmetic progression (AP) is a sequence of numbers in which each term is obtained by adding a fixed number ‘d’ to the preceeding term, except the first term.
The fixed number is called the common difference. It can be positive, negative or zero.
Any Arithmetic progression can be represented as :
a, a + d, a + 2d, a + 3d,…..
where ‘a’ is the first term and ‘d’ is the common difference. Arithmetic progressions which does not have a last term are called Infinite Arithmetic Progression. e.g.:
6, 9, 12, 15,…….
Formula for common Difference (d)
A sequence of numbers a1, a2, a3…. is an AP if the difference a2 – a1, a3 – a2, a4 – a3…. gives the same value, i.e. if ak+1 – ak is the same for different values of k. The difference (ak+1 – ak) is called common difference (d). Here ak+1 and ak are the (k + 1)th and kth terms respectively.
∴ d = a2 – a1 = a3 – a2 = a4 – a3
nth Term (or General Term) of an Arithmetic Progressions
In an AP, with first term ‘a’ and common difference d, the nth term(or the general term) is given by,
an = a + (n – 1)d
Note that an AP can be finite or infinite according to as the number of terms are finite or infinite.
If there are m terms in an AP then am is the last term and is sometimes denoted by ‘l’.
Sum of the FIRST ‘n’ Terms of an A.P.
(i) The sum of the first n terms of an A.P. is given by

where a is the first term and d is the common difference
(ii) If l is the last term of the finite A.P. say the nth term, then the sum of all terms of the A.P. is given by,
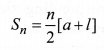
Note that sum of first n positive integers is given by
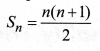
Arithmetic Mean Between Two Numbers
If a, b, c are in AP. Then b is called the arithmetic mean of a and c and is given by
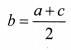
CLASS 10 MATHS CHAPTER 5 EXERCISE 5.1 AP SOLUTIONS IN HINDI












Comments are closed