NCERT Solutions For Class 6 Maths Chapter 11 Algebra Ex 11.1
Exercise 11.1
Ex 11.1 Class 6 Maths Question 1.
Find the rule which gives the number of matchsticks required to make the following matchsticks patterns. Use a variable to write the rule.
(a) A pattern of letter T as T
(b) A pattern of letter Z as Z
(c) A pattern of letter U as U
(d) A pattern of letter V as V
(e) A pattern of letter E as E
(f) A pattern of letter S as S
(g) A pattern of letter A as A
Solution:
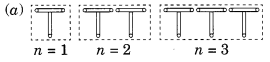
Number of matchstieks required to make the pattern of T
For n = 1 is 2 x n
For n = 2 is 2 x n
For n = 3 is x n
∴ Rule is 2n where n is number of Ts.
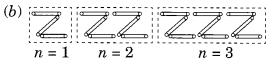
Number of matchstieks required to make the pattern of Z.
For n = 1 is 3 x n
For n = 2 is 3 x n
For n = 3 is 3 x n
∴ Rule is 3n where n is number of Zs.
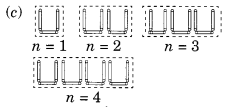
Number of matchstieks required to make the pattern U.
For n = 1 is 3 x n
For n = 2 is 3 x n
For n = 3 is 3 x n
For n = 4 is 3 x n
∴ Rule is 3n where n is number of Us.
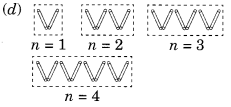
Number of matchstieks required
For n = 1 is 2 x n
For n = 2 is 2 x n
For n = 3 is 2 x n
For n = 4 is 2 x n
∴ Rule is 2n where n is number of Vs.
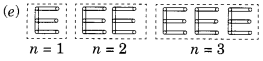
Number of matchstieks required
For n = 1 is 5 x n
For n = 2 is 5 x n
For n = 3 is 5 x n
∴ Rule is 5n where n is number of Es.
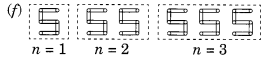
Number of matchstieks required
For n = 1 is 5 x n
For n = 2 is 5 x n
For n = 3 is 5 x n
∴ Rule is 5n where n is number of Ss.
Number of matchstieks required
For n = 1 is 6 x n
For n = 2 is 6 x n
For n = 3 is 6 x n
∴ Rule is 6n where n is number of As.
Ex 11.1 Class 6 Maths Question 2.
We already know the rule for the pattern of letters L, C and F. Some of the letters from Ql. (given above) give us the same rule as that given by L. Which are these? Why does this happen?
Solution:
Rule for the following letters
For L it is 2n
For C it is 2n
For V it is 2n
For F it is 3n
For T it is 3n
For U it is 3n
We observe that the rule is same of L, V and T as they required only 2 matchstieks.
Letters C, F and U have the same rule, i.e., 3n as they require only 3 sticks.
Ex 11.1 Class 6 Maths Question 3.
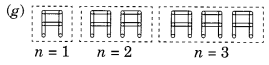
Cadets are marching in a parade. There are 5 cadets in a row. What is the rule which gives the number of cadets, given the number of rows? (use n for the number of rows.)
Solution:
Number of cadets in a row = 5
Number of rows = n
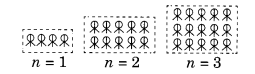
Number of cadets
For n = 1 is 5 x n
For n = 2 is 5 x n
For n = 3 is 5 x n
∴ Rule is 5n where n is the number of rows.
Ex 11.1 Class 6 Maths Question 4.
If there are 50 mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? (Use b for the number of boxes.)
Solution:
Number of boxes = b
Number of mangoes in a box = 50
Number of mangoes,
For n = 1 is 50 x b
For n = 2 is 50 x b
For n = 3 is 50 x b
∴ Rule is 50b where b represents the number of boxes.
Ex 11.1 Class 6 Maths Question 5.
The teacher distributes 5 pencils per student. Can you tell how many pencils are needed, given the number of students? (Use s for the number of students.)
Solution:
Number of students = s
Number of pencils distributed per students = 5
Number of pencils required
For n = 1 is 5 x s
For n = 2 is 5 x s
For n = 3 is 5 x s
∴ Rule is 5s where s represents the number of students.
Ex 11.1 Class 6 Maths Question 6.
A bird flies 1 kilometre in one minute. Can you express the distance covered by the bird in terms of is flying time in minutes? (Use t for flying time in minutes.)
Solution:
Distance covered in 1 minute = 1 km.
The flying time = t
Distance covered
For n = 1 is 1 x t km
For n = 2 is 1 x t km
For n = 3 is 1 x t km
∴ Rule is 1.t km where t represents the flying time.
Ex 11.1 Class 6 Maths Question 7.
Radha is drawing a dot Rangoli (a beautiful pattern of lines joining dots with chalk powder. She has a dots in a row. How many dots will her rangoli have for r rows? How many dots are there if there are 8 rows? If there are 10 rows?
Solution:
Number of rows = r
Number of dots in a row drawn by Radha = 8
∴ The number of dots required
For r = 1 is 8 x r
For r = 2 is 8 x r
For r = 3 is 8 x r
∴ Rule is 8r where r represents the number of rows.
For r = 8, the number of dots = 8 x 8 = 64
For r = 10, the number of dots = 8 x 10 = 80
Ex 11.1 Class 6 Maths Question 8.
Leela is Radha’s younger sister. Leela is 4 years younger than Radha. Can you write Leela’s age in terms of Radha’s age? Take Radha’s age to be x years.
Solution:
Radha’s age = x yeas.
Given that Leela’s age
= Radha’s age – 4 years
= x years – 4 years
= (x – 4) years
Ex 11.1 Class 6 Maths Question 9.
Mother has made laddus. She gives some laddus to guests and family members, still 5 laddus remain. If the number of laddus mother gave away is l, how many laddus did she make?
Solution:
Given that the number of laddus given away = l
Number of laddus left = 5
∴ Number of laddus made by mother = l + 5
Ex 11.1 Class 6 Maths Question 10.
Oranges are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still 10 oranges remain outside. If the number of oranges in a small box are taken to be x, What is the number of oranges in the larger box?
Solution:
Given that, the number of oranges in smaller box = x
∴ Number of oranges in bigger box = 2(number of oranges in small box) + (Number of oranges remain outside)
So, the number of oranges in bigger box = 2x + 10
Ex 11.1 Class 6 Maths Question 11.
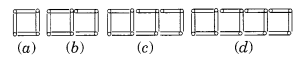
(a) Look at the following matchstick pattern of square. The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares.
(Hint: If you remove the vertical stick at the end, you will get a pattern of Cs)
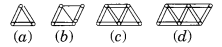
(b) Following figure gives a matchstick pattern of triangles. As in Exercise 11(a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.
Solution:
(a) Let n be the number of squares.
∴ Number of matchsticks required
For n = 1 is 3 x n + l = 3n + 1 = 4
For n = 2is 3 x n + l = 3n + 1 = 7
For n = 3is 3 x n + l = 3n + 1 = 10
For n = 4is 3 x n + l = 3n + 1 = 13
∴ Rule is 3n + 1 where n represents the number of squares.
(b) Let n be the number of triangles.
∴ Number of matchsticks required
For n = 1 is 2n + 1 = 3
For n = 2 is 2n + 1 = 5
For n = 3 is 2n + 1 = 7
For n = 4 is 2n + 1 = 9
∴ Rule is 2n + 1 where n represents the number of matchsticks.







<!– –>
Comments are closed