NCERT Solutions for Class 7 Maths Chapter 1 Integers Ex 1.3
NCERT Solutions for Class 7 Maths Chapter 1 Integers Exercise 1.3
Ex 1.3 Class 7 Maths Question 1.
Find each of the following products:
(a) 3 × (-1)
(b) (-1) × 225
(c) (-21) × (-30)
(d) (-316) × (-1)
(e) (-15) × 0 × (-18)
(f) (-12) × (-11) × (10)
(g) 9 × (-3) × (-6)
(h) (-18) × (-5) × (-4)
(i) (-1) ×(-2) × (-3) × 4
(j) (-3) × (-6) × (-2) × (-1)
Solution:
(a) 3 × (-1) = -3 × 1 = -3
(b) (-1) × 225 = -1 × 225 = -225
(c) (-21) × (-30) = (-) × (-) × 21 × 30 = 630
(d) (-316) × (-1) = (-) × (-) × 316 × 1 = 316
(e) (-15) × 0 × (-18) = 0 [∵ a × 0 = a]
(f) (-12) × (-11) × (10)
= (-) × (-) × 12 × 11 × 10 = 1320
(g) 9 × (-3) × (-6) = (-3) × (-6) × 9
= (—) × (-) × 3 × 6 × 9 = 162
(h) (-18) × (-5) × (-4)
= (-) × (-) × (-) × 18 × 5 × 4 = -360
(i) (-1) × (-2) × (-3) × 4
= (-) × (-) × (-) × 1 × 2 × 3 × 4 = -24
(j) (-3) × (-6) × (-2) × (-1)
= (-) × (-) × (-) × (-) × 3 × 6 × 2 × 1 = 36
Ex 1.3 Class 7 Maths Question 2.
Verify the following:
(a) 18 × [7 + (-3)] = [18 × 7] + [18 × (-3)]
(b) (-21) × [(-4) + (-6)] = [(-21) × (-4)] + [(-21) × (-6)]
Solution:
(a) 18 × [7 + (-3)] = [18 × 7] + [18 × (-3)]
LHS = 18 × [7 + (-3)] = 18 × 4 = 72
RHS = [18 × 7] + [18 × (-3)] = 126 + (-54)
= 126 – 54 = 72
LHS = RHS
Hence, verified.
(b) (-21) × [(-4) + (-6)] = [(-21) × (-4)] + [(-21) × (-6)]
LHS = (-21) × [(-4) + (-6)]
= (-21) × (-10)
= (-) × (-) × 21 × 10 = 210
RHS = [(-21) × (-4)] + [(-21) × (-6)]
= (84) + (126) = 84 + 126 = 210
LHS = RHS
Hence, verified.
Ex 1.3 Class 7 Maths Question 3.
(i) For any integer a, what is (-1) × a equal to?
(ii) Determine the integer whose product with (-1) is 0.
(a) -22
(b) 37
(c) 0
Solution:
(i) (-1) × a = -a
(ii) (-1) × 0 = 0 [∵ a × 0 = 0]
Hence (c) 0 is the required integer.
Ex 1.3 Class 7 Maths Question 4.
Starting from (-1) × 5, write various products showing some pattern to show (-1) × (-1) = 1
Solution:
(-1) × 5 = -5
(-1) × 4 = -4 = (-5) + 1
(-1) × 3 = -3 = (-4) + 1
(-1) × 2 = -2 = (-3) + 1
(-1) × (1) = -1 = (-2) + 1
(-1) × 0 = 0 – (-1) + 1
(-1) × (-1) = 1 = 0+1
Ex 1.3 Class 7 Maths Question 5.
Find the product, using suitable properties:
(a) 26 × (-48) + (-48) × (-36)
(b) 8 × 53 × (-125)
(c) 15 × (-25) × (-4) × (-10)
(d) (-41) × 102
(e) 625 × (-35) + (-625) × 65
(f) 7 × (50 – 2)
(g) (-17) × (-29)
(h) (-57) × (-19) + 57
Solution:
(a) 26 × (-48) + (-48) × (-36)
= -48 × [26 + (-36)] = -48 × [26 – 36] = -48 × -10 = 480 [Distributive property of multiplication over
addition]
(b) 8 × 53 × (-125) = 53 × [8 × (-125)]
[Associative property of multiplication] = 53 × (-1000) = -53000
(c) 15 × (-25) × (-4) × (-10)
= [(-25) × (-4)] × [15 × (-10)]
[Regrouping the terms] = 100 × (-150) = -15000
(d) (-41) × 102 = (-41) × [100 + 2]
= (-41) × 100 + (-41) × 2
[Distributive property of multiplication over addition] = -4100 – 82 = -4182
(e) 625 × (-35) + (-625) × 65
= 625 × [(-35) + (-65)]
[Distributive property of multiplication over addition]
= 625 × (-100) = -62500
(f) 7 × (50 – 2) = 7 × 48 = 336 or
7 × (50 – 2) = 7 × 50 -7 × 2 = 350 – 14 = 336 [Distributive property of multiplication over addition]
(g) (-17) × (-29) = (-17) × [30 + (-1)]
= (-17) × 30 + (-17) × (-1)
= -510 + 17 = -493
[Distributive property of multiplication over addition]
(h) (-57) × (-19) + 57 = 57 × 19 + 57
= 57 × 19 + 57 × 1 [Y (-) × (-) = (+)] [Distributive property of multiplication over addition]
= 57 × (19 + 1) = 57 × 20 = 1140
Ex 1.3 Class 7 Maths Question 6.
A certain freezing process requires that room temperature be lowered from 40°C at the rate of 5°C every hour. What will be the room temperature 10 hours after the process begins?
Solution:
Temperature of the room in the beginning = 40°C
Temperature after 1 hour
= 40°C – 1 × 5°C = 40°C – 5°C – 35°C
Similarly, temperature of the room after 10 hours
= 40°C – 10 × 5°C = 40°C – 50°C = -10°C
Ex 1.3 Class 7 Maths Question 7.
In a class test containing 10 questions, 5 marks are awarded for every correct answer and (-2) marks are awarded for every incorrect answer and 0 for questions not attempted.
(i) Mohan gets four correct and si× incorrect answers. What is his score?
(ii) Reshma gets five correct answers and five incorrect answers, what is her score?
(iii) Heena gets two correct and five incorrect answers out of seven questions she attempts. What is her score?
Solution:
(i) Marks awarded to Mohan = 4 × 5
=20 for correct answers Marks awarded to Mohan = 6 × (-2)
= -12 for incorrect answers.
∴ Total marks obtained by Mohan
= 20 + (-12) = 20 – 12 = 8
(ii) Marks awarded to Reshma for correct answers
= 5 × 5 = 25
Marks awarded to Reshma for incorrect answers
= 5 × (-2) = -10
∴ Total marks obtained by Reshma
= 25 + (-10) = 25 – 10 = 15
(iii) Marks awarded to Heena for correct answers
= 2 × 5 = 10
Marks awarded to Heena for incorrect answers
= 5 × (-2) = -10
Number of question not attempted by Heena
= 10 – (2 + 5) = 10 – 7 = 3
Marks awarded to Heena for non-attempted questions
=3×0=0
∴ Total marks obtained by Heena
= 10 + (-10) + 0 = 10-10+ 0 = 0
Ex 1.3 Class 7 Maths Question 8.
A cement company earns a profit of ₹ 8 per bag of white cement sold and a loss of ₹ 5 per bag of grey cement sold.
(a) The company sells 3,000 bags of white cement and sold 5,000 bags of grey cement in a month. What is its profit or loss?
(b) What is the number of white cement bags it must sell to have neither profit nor loss, if the number of grey bags sold is 6,400 bags.
Solution:
(a) Profit on one white cement bag = ₹ 8
loss on one grey cement bag = ₹ – 5
Profit on 3,000 bags of white cement
= ₹ (8 × 3,000) = ₹ 24,000
Loss on 5,000 bags of grey cement
= ₹ (-5 × 5000) = – ₹ 25,000
Total loss = – ₹ 25,000 + ₹ 24,000
= – ₹ 1000 i.e. ₹ 1000
(b) Selling price of grey bags at a loss of ₹ 5
= ₹ (5 × 6,400) – ₹ 32,000
For no profit and no loss, the selling price of white bags = ₹ 32,000
Rate of selling price of white bags at a profit of ₹ 8 per bag.
∴ Number of white cement bags sold
(=frac{32000}{8}=4000)
Hence, the required number of bags = 4,000
Ex 1.3 Class 7 Maths Question 9.
Replace the blank with an integer to make it a true statement.
(a) (-3) × __ = 27
(b) 5 × __ = -35
(c) __ × (-8) = -56
(d) __ × (-12) = 132
Solution:
(a) (-3) × __ = 27 = (-3) × (-9) = 27 [∵ (-) × (-) = (+)]
(b) 5 × __ = -35 = 5 × (-7) = -35 [∵ (+) × (-) = (-)]
(c) __ × (-8) = -56 = 7 × (-8) = -56 [∵ (+) × (-) = (-)]
(d) __ × (-12) = 132 = (-11) × (-12) = 132 [∵ (-) × (-) = (+)]

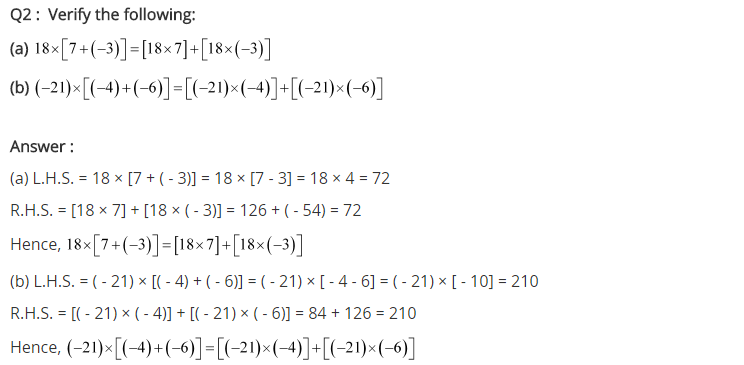









<!– –>
Comments are closed