NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4
NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Exercise 6.4
Ex 6.4 Class 8 Maths Question 1.
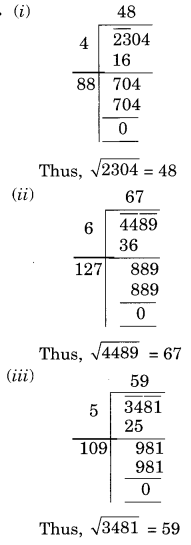
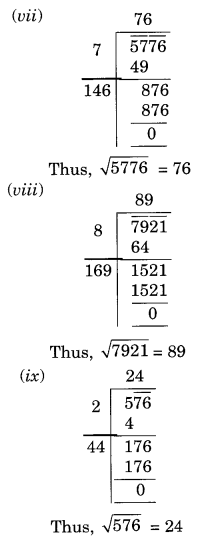
Find the square root of each of the following numbers by Long Division method.
(i) 2304
(ii) 4489
(iii) 3481
(iv) 529
(v) 3249
(vi) 1369
(vii) 5776
(viii) 7921
(ix) 576
(x) 1024
(xi) 3136
(xii) 900
Solution:
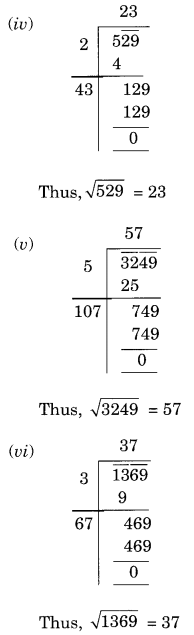
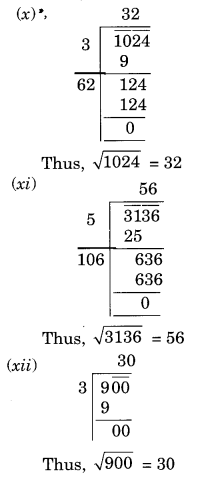
Ex 6.4 Class 8 Maths Question 2.
Find the number of digits in the square root of each of the following numbers (without any calculation)
(i) 64
(ii) 144
(iii) 4489
(iv) 27225
(v) 390625
Solution:
We know that if n is number of digits in a square number then
Number of digits in the square root = (frac { n }{ 2 }) if n is even and (frac { n+1 }{ 2 }) if n is odd.
(i) 64
Here n = 2 (even)
Number of digits in √64 = (frac { 2 }{ 2 }) = 1
(ii) 144
Here n = 3 (odd)
Number of digits in square root = (frac { 3+1 }{ 2 }) = 2
(iii) 4489
Here n = 4 (even)
Number of digits in square root = (frac { 4 }{ 2 }) = 2
(iv) 27225
Here n = 5 (odd)
Number of digits in square root = (frac { 5+1 }{ 2 }) = 3
(iv) 390625
Here n = 6 (even)
Number of digits in square root = (frac { 6 }{ 2 }) = 3
Ex 6.4 Class 8 Maths Question 3.
Find the square root of the following decimal numbers.
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36
Solution:
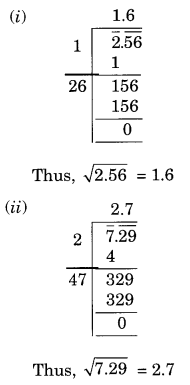
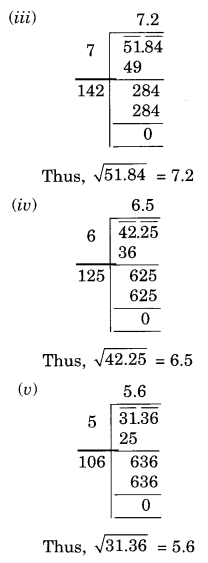
Ex 6.4 Class 8 Maths Question 4.
Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 402
(ii) 1989
(iii) 3250
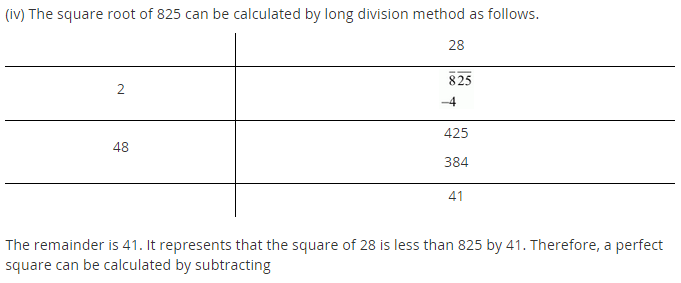
(iv) 825
(v) 4000
Solution:
(i)
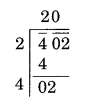
Here remainder is 2
2 is the least required number to be subtracted from 402 to get a perfect square
New number = 402 – 2 = 400
Thus, √400 = 20
(ii)
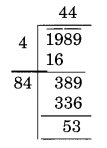
Here remainder is 53
53 is the least required number to be subtracted from 1989.
New number = 1989 – 53 = 1936
Thus, √1936 = 44
(iii)
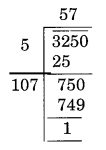
Here remainder is 1
1 is the least required number to be subtracted from 3250 to get a perfect square.
New number = 3250 – 1 = 3249
Thus, √3249 = 57
(iv)
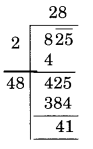
Here, the remainder is 41
41 is the least required number which can be subtracted from 825 to get a perfect square.
New number = 825 – 41 = 784
Thus, √784 = 28
(v)
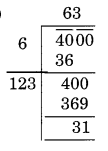
Here, the remainder is 31
31 is the least required number which should be subtracted from 4000 to get a perfect square.
New number = 4000 – 31 = 3969
Thus, √3969 = 63
Ex 6.4 Class 8 Maths Question 5.
Find the least number which must be added to each of the following numbers so as to get a perfect square. Also, find the square root of the perfect square so obtained.
(i) 525
(ii) 1750
(iii) 252
(iv) 1825
(v) 6412
Solution:
(i)
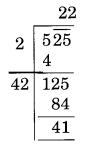
Here remainder is 41
It represents that square of 22 is less than 525.
Next number is 23 an 232 = 529
Hence, the number to be added = 529 – 525 = 4
New number = 529
Thus, √529 = 23
(ii)
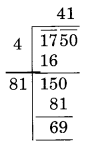
Here the remainder is 69
It represents that square of 41 is less than in 1750.
The next number is 42 and 422 = 1764
Hence, number to be added to 1750 = 1764 – 1750 = 14
Require perfect square = 1764
√1764 = 42
(iii)
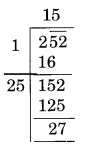
Here the remainder is 27.
It represents that a square of 15 is less than 252.
The next number is 16 and 162 = 256
Hence, number to be added to 252 = 256 – 252 = 4
New number = 252 + 4 = 256
Required perfect square = 256
and √256 = 16
(iv)
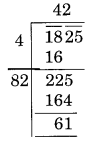
The remainder is 61.
It represents that square of 42 is less than in 1825.
Next number is 43 and 432 = 1849
Hence, number to be added to 1825 = 1849 – 1825 = 24
The required perfect square is 1848 and √1849 =43
(v)
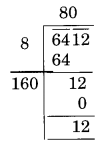
Here, the remainder is 12.
It represents that a square of 80 is less than in 6412.
The next number is 81 and 812 = 6561
Hence the number to be added = 6561 – 6412 = 149
The require perfect square is 6561 and √6561 = 81
Ex 6.4 Class 8 Maths Question 6.
Find the length of the side of a square whose area = 441 m2
Solution:
Let the length of the side of the square be x m.
Area of the square = (side)2 = x2 m2
x2 = 441 ⇒ x = √441 = 21
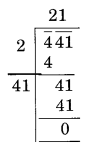
Thus, x = 21 m.
Hence the length of the side of square = 21 m.
Ex 6.4 Class 8 Maths Question 7.
In a right triangle ABC, ∠B = 90°.
(a) If AB = 6 cm, BC = 8 cm, find AC
(b) If AC = 13 cm, BC = 5 cm, find AB
Solution:
(a) In right triangle ABC
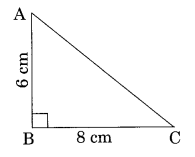
AC2 = AB2 + BC2 [By Pythagoras Theorem]
⇒ AC2 = (6)2 + (8)2 = 36 + 64 = 100
⇒ AC = √100 = 10
Thus, AC = 10 cm.
(b) In right triangle ABC
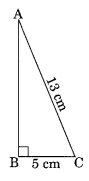
AC2 = AB2 + BC2 [By Pythagoras Theorem]
⇒ (13)2 = AB2 + (5)2
⇒ 169 = AB2 + 25
⇒ 169 – 25 = AB2
⇒ 144 = AB2
AB = √144 = 12 cm
Thus, AB = 12 cm.
Ex 6.4 Class 8 Maths Question 8.
A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain the same. Find the minimum number of plants he needs more for this.
Solution:
Let the number of rows be x.
And the number of columns also be x.
Total number of plants = x × x = x2
x2 = 1000 ⇒ x = √1000
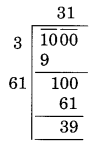
Here the remainder is 39
So the square of 31 is less than 1000.
Next number is 32 and 322 = 1024
Hence the number to be added = 1024 – 1000 = 24
Thus the minimum number of plants required by him = 24.
Alternative method:
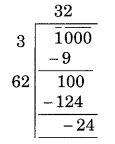
The minimum number of plants required by him = 24.
Ex 6.4 Class 8 Maths Question 9.
There are 500 children in a school. For a P.T. drill, they have to stand in such a manner that the number of rows is equal to the number of columns. How many children would be left out in this arrangement?
Solution:
Let the number of children in a row be x. And also that of in a column be x.
Total number of students = x × x = x2
x2 = 500 ⇒ x = √500
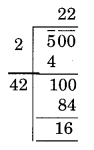
Here the remainder is 16
New Number 500 – 16 = 484
and, √484 = 22
Thus, 16 students will be left out in this arrangement.















<!– –>
Comments are closed