पाठ 14, सांख्यिकी

परिभाषा

• हम जानते हैं कि संख्यात्मक या अन्य तथ्य या चित्र जिन्हें आंकड़े (data) कहते हैं एक खास उद्देश्य से एकत्रित किए जाते हैं। Data लैटिन शब्द datum का बहुवचन है।
• Statistics शब्द लैटिन शब्द status से बना है जिसका अर्थ एक (राजनैतिक) राज्य होता है।
• सांख्यिकी का काम आंकड़ों का संग्रह करना, संगठित करना, विश्लेषित करना और निर्वचन करना है।

आंकड़ों का संग्रह

आंकड़े दो प्रकार के होते हैं। एक प्राथमिक आंकड़े और दूसरे गौण आंकड़े।

• प्राथमिक आंकड़ेः जब अन्वेषक ने अपने दिमाग में एक निश्चित उद्देश्य रखकर सूचनाओं को एकत्रित किया हो तो इस प्रकार एकत्रित किए गए आंकड़ों को प्राथमिक आंकड़े कहा जाता है।
• गौण आंकड़े: जब किसी स्रोत से, जिसमें सूचनाएं पहले से ही एकत्रित हैं, आंकड़े प्राप्त किए गए हों तो उन आंकड़ों को गौण आंकड़े कहा जाता है।
• इस प्रकार के आंकड़े का प्रयोग, जिसे किसी और ने इन्हें अन्य संदर्भ में एकत्रित किया है, यह सुनिश्चित करने के बाद ही कि ये स्रोत विश्वसनीय हैं, काफी सावधानी के साथ करना चाहिए।

आंकड़ों का प्रस्तुतीकरण

आंकड़ों का संग्रह करने के बाद अन्वेषक को इन आंकड़ों को ऐसे रूप में प्रस्तुत करने की विधियों को ज्ञात करना होता है जो अर्थपूर्ण हों और सरलता से समझी जा सकती हों।

76        54        25        95        60        44        75        78        35        62

आंकड़ों के इस रूप को यथा प्राप्त आंकड़े कहते हैं।

छात्रों द्वारा प्राप्त न्यूनतम अंक 25 है और छात्रों द्वारा प्राप्त अधिकतम अंक 95 है।

आंकड़ों को आरोही क्रम या अवरोही क्रम में लिखने पर काफी समय लग सकता है, विशेष रूप से तब, जबकि प्रयोग में प्रेक्षणों की संख्या अधिक हो, जैसा कि अगले उदाहरण में आप देख सकते हैं।

25        35        44        54        60        62        75        76        78        95

आंकड़ों के अधिकतम और न्यूनतम मानों के बीच का अंतर को आंकड़ों का परिसर कहा जाता है।

अतः, इस उदाहरण में परिसर 95 – 25 = 70 है।

बारंबरता

6          7          5          7          7          8          7          6          10        7

4          10        6          8          8          9          5          6          4          8

9

अतः 10 की बारंबरता 2 है।

एक निश्चित अंक प्राप्त करने वाले विद्यार्थियों की संख्या को इस अंक की बारंबरता कहा जाता है।

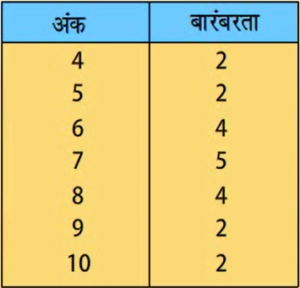
इस सारणी को अवर्गीकृत बारंबरता बंटन सारणी या केवल बारंबरता बंटन सारणी कहा जाता है।

वर्गीकृत बारंबरता बंटन सारणी

1, 1, 1, 4, 4, 5, 5, 5, 6, 7, 8, 8, 8, 9, 9, 9, 9, 9, 9, 10, 10, 11, 12, 12, 13, 14, 14, 15, 15, 16, 16, 16, 16, 17, 17, 17, 18, 18

इन वर्गों को वर्ग या वर्ग अंतराल कहते हैं और माप को वर्ग माप या वर्ग चौड़ाई कहा जाता है।

यहां माप 4 है।

इन सभी वर्गों में सबसे छोटी संख्या को निम्न वर्ग सीमा और सबसे बड़ी संख्या को उपरि वर्ग सीमा कहते हैं।

जैसे, 0- 3, 0 निम्न वर्ग सीमा है और 3 उपरि वर्ग सीमा है।

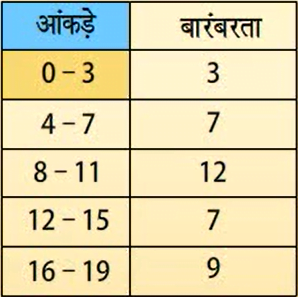
इस प्रकार की सारणियों को वर्गीकृत बारंबरता बंटन सारणी कहते हैं।

आंकड़ों का आलेखीय निरूपण

जब आंकड़ों को सीखने वालों के सामने चित्रात्मक (या आलेखीय) रूप में निरूपित किया जाता है तो यह निरूपण को ज्यादा दर्शनीय और समझने योग्य बनाता है।

आंकड़ों को आलेखीय रूप में निरूपित करने के कई प्रकार हैं।

• (क) दण्ड आलेख
• (ख) एकसमान चौड़ाई और परिवर्ती चौड़ाइयों वाले आयतचित्र
• (ग) बारंबरता बहुभुज

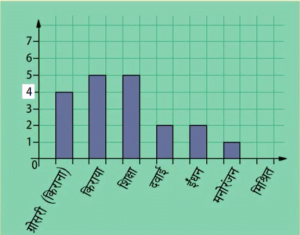
दण्ड आलेखः दण्ड आलेख आंकड़ों का एक चित्रीय निरूपण होता है जिसमें प्रायः एक अक्ष (मान लीजिए x अक्ष) पर एक चर को प्रकट करने वाले एक समान चौड़ाई के दण्ड खींचे जाते हैं जिनके बीच में बराबर-बराबर दूरियां छोड़ी जाती हैं। चर के मान दूसरे अक्ष (मान लीजिए y अक्ष) पर दिखाए जाते हैं और दण्डों की ऊंचाईयां चर के मानों पर निर्भर करती हैं।

किस दिन उसने सबसे अधिक चाकलेट खाई थी?

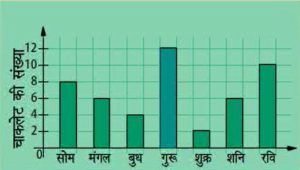
दण्ड आलेख का निरूपण

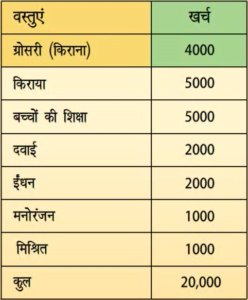
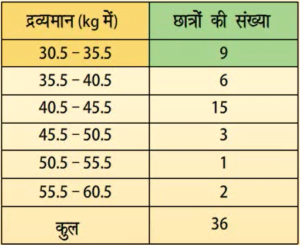
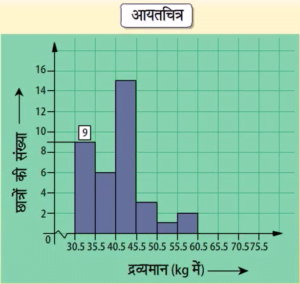
आयतचित्र

बारंबरता बहुभुज

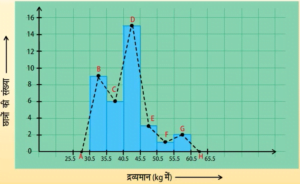
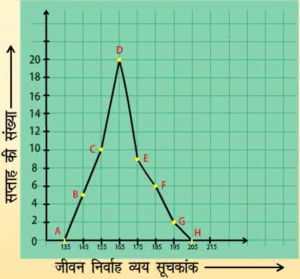
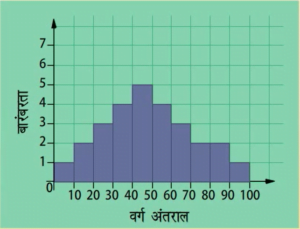
आयतचित्र बनाए बिना ही बारंबरता बहुभुजों को स्वतंत्र रूप से भी बनाया जा सकता है। इसके लिए हमें आंकड़ों में प्रयुक्त वर्ग अंतरालों के मध्य-बिन्दुओं की आवश्यकता होती है। वर्ग अंतरालों के इन मध्य-बिंदुओं को वर्ग-चिह्न कहा जाता है। वर्ग अंतराल के वर्ग-चिहुन प्राप्त करने के लिए हमें सभी उपरि सीमाओं और निम्न सीमाओं का योग करके उसे 2 से विभाजित कर देते हैं।

बारंबरता बहुभुज समान प्रकृति के दो अलग-अलग आंकड़ों की तुलना करने में बहुत उपयोगी होता है। जैसे, एक ही विद्यालय के दो फुटबाल टीमों के प्रदर्शन की तुलना।

केन्द्रीय प्रवृत्ति के माप

केन्द्रीय प्रवृत्ति का आशय आंकड़ों के माध्य या किसी खास मान से होता है और इसका मापन माध्य, माध्यक और बहुलक से किया जाता है। आइए एक-एक कर इनके बारे में जानें।

माध्यः अनेक प्रेक्षणों का माध्य (या औसत) सभी प्रेक्षणों के मानों के योग को प्रेक्षणों की कुल संख्या से भाग देने पर प्राप्त होता है।

माध्यकः माध्यक दिए हुए प्रेक्षणों में वह मान होता है जो इसे ठीक-ठीक दो भागों में विभक्त कर देता है।

जब प्रेक्षणों की संख्या n विषम होती है, तब माध्यक 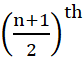 प्रेक्षण का मान होता है।

उदाहरण के लिए, यदि n = 13 है तो 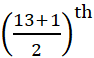 माध्यमक होगा जो कि 7th प्रेक्षण है।

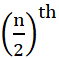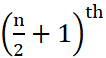और प्रेक्षणों की संख्या n सम होती है, तब माध्यक  और  प्रेक्षणों का माध्य होता है।

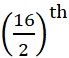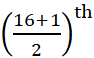उदाहरण के लिए, यदि n = 16 हो तो  और  प्रेक्षणों के मानों का माध्य

अर्थात 8th और 9th प्रेक्षणों के मानों का माध्य ही माध्यक होगा।

बहुलक: बहुलक प्रेक्षण का वह मान होता है जो बार-बार घटित होता रहता है, अर्थात अधिकतम बारंबरता वाले प्रेक्षण को बहुलक कहा जाता है।

माउण्ट राइवल प्रत्येक वर्ष एक फुटबाल प्रतियोगिता आयोजित करता है। इस वर्ष 10 वें खेल में घरेलु टीम की ओर से सबसे अधिक गोल करने वाले ने 7, 5, 0, 7, 8, 5, 5, 4, 4 और 5 गोल किए। माध्य स्कोर क्या है?

आइए हम एक चर xi का प्रयोग करें जो कि i वें प्रेक्षण को प्रकट करता है। इस स्थिति में i का मान 1 से 10 के बीच हो सकता है। अतः हमारा पहला प्रेक्षण x1 है, और दूसरा प्रेक्षण x2 है और x10 तक सभी मान इसी प्रकार होंगे।

यहां x1 = 7 पहले प्रक्षेण का मान है।

इसी प्रकार x2 = 5, x3 = 0, x4 = 7, x5 = 8, x6 = 5, x7 = 5, x8 = 4, x9 = 4 और x10 = 5

अतः माध्य

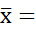
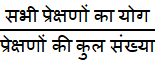
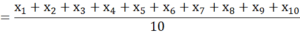
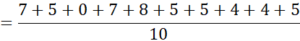
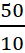=  = 5 अतः माध्य स्कोर 5 है।

x1 + x2 + x3 +………..+ x30

अतः x1 + x2 + x3 +………..+ x30 लिखने के बजाय हम इसे x का योग लिखते हैं जहां

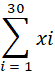
यह अवर्गीकृत बारंबरता के लिए है।

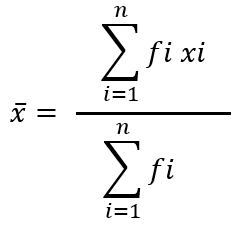
20 छात्रों द्वारा प्राप्त अंको (10 में से) का बहुलक ज्ञात कीजिए:

4,6,5,9,3,2,7,7,6,5,4,9,10,10,3,4,7,6,9,9

हम जानते हैं कि बहुलक उस प्रेक्षण का मान है जिसकी बारंबरता अधिकतम होती है।

4,6,5,9,3,2,7,7,6,5,4,9,10,10,3,4,7,6,9,9

आरोही क्रम

2,3,3,4,4,4,5,5,6,6,6,7,7,7,9,9,9,9,10,10

9 अंको का बहुलक है।

Statistics (सांख्यिकी)

Statistics शब्द लैटिन के “Status” या इटैलियन शब्द “Statista” से आया है। इन शब्दों

का अर्थ “राजनैतिक राज्य” या सरकार होता है। शेक्सपीयर ने अपने नाटक हैमलेट (1602) में Statistics शब्द का प्रयोग किया है। पुराने समय में सांख्यिकी का प्रयोग शासकों द्वारा किया जाता था। लेकिन सांख्यिकी का प्रयोग शासकों और राजाओं तक ही सीमित था जो इसका प्रयोग अपने सैनिक क्षमता, संपत्ति, करों और दूसरे सरकारी मदों के आंकलन के लिए अपने राज्य की भूमि, कृषि, वाणिज्य, जनसंख्या की गणना के लिए किया करते थे।

सारांश

एक निश्चित उद्देश्य से एकत्रित किए गए तथ्यों और अंकों को आंकड़ा कहते हैं। ८) सांख्यिकी अध्ययन का वो क्षेत्र है जिसमें आंकड़ों के प्रति प्रस्तुतिकरण, विश्लेषण तथा निर्वचन पर विचार किया जाता है?

अवर्गीकृत आंकड़ों की केन्द्रीय प्रवृत्ति की तीन माप हैं: माध्यः प्रेक्षणों के सभी मानों के योग को प्रेक्षणों की कुल संख्या से भाग देने पर माध्य प्राप्त हो जाता है। इसमे x प्रकट किया जाता है।

माध्यकः माध्यक सबसे मध्य वाले प्रेक्षण का मान होता है। जब प्रेक्षणों की संख्या n विषम होती है, तब माध्यक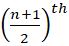

प्रेक्षण का मान होता है। प्रेक्षणों और यदि प्रेक्षणों की संख्या n सम होती है, तब माध्यक 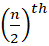और 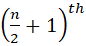 का माध्य होता है।

बहुलकः सबसे अधिक बारंबरता वाला प्रेक्षण बहुलक होता है।