पाठ 15, प्रायिकता

 प्रायिकता

गणित की वह शाखा, जिसमे घटनाओं के घटित होने की संभावनाओं का संख्यात्मक अध्ययन किया जाता है, वह प्रायिकता कहलाता है. प्रायिकता सिद्धांत के विकाश में निम्नलिखित गणितज्ञों का योगदान रहा है.

• जैकाब बरनौली (1654 – 1705)
• डी मायवर (1667 – 1754)
• लाप्लस (1749 – 1827)
• प्वासो (1781 – 1840)
• ए. कॉलमोगोरोव (1703 – 1987)

इस सिद्धांत का जन्म जुआ के खेल से हुआ. इसका प्रयोग इन्गिनीरिंग के विभिन्न क्षेत्रों; जैसे – समुंद्री रास्तें में जहाजों का बर्ताव में होता है.

यादृच्छिक प्रयोग

वैसा प्रयोग, जिसके परिणाम किसी नियम का पालन न करे, वह यादृच्छिक प्रयोग कहलाता है. जैसे;

किसी पासे को फेकना एक यादृच्छिक प्रयोग है, क्योंकि इसपर 6 फलक होते है, जिस पर क्रमशः 1, 2, 3, 4, 5, 6 अंकित रहते है. इसे फेकने पर कौन सी संख्या आएगा, इसकी कोई निश्चिता नही है. उसी प्रकार थैले में रखे विभिन्न रंगों की गोलियों में से एक गोली निकलना यादृच्छिक प्रयोग है.

प्रायिकता समष्टि

किसी यादृच्छिक प्रयोग से प्राप्त सभी संभव परिणाम को Prayikta समष्टि कहते है. इसे प्रतिदर्श समष्टि भी कहा जाता है. इसे प्रायः S से व्यक्त किया जाता है. जैसे;

पासे को फेंकने से बना प्रायिकता समष्टि = {1, 2, 3, 4, 5, 6}

सिक्के को उछालने से बनी प्रतिदर्श समष्टि = {H, T}

2 सिक्के को उछालने से बनी प्रतिदर्श समष्टि = {HH, HT, TH, TT}

प्रायिकता से सम्बंधित महत्वपूर्ण अवधारणा

घटना बिंदु (Event Point): प्रतिदर्श समष्टि के प्रत्येक अवयव घटना बिंदु कहलाता है.

जैसे;

S = {1, 2, 3, 4, 5, 6}, इसमें 1, 2, 3, 4, 5, और 6 घटना बिंदु है.

विविक्त प्रतिदर्श समष्टि: जिस प्रतिदर्श समष्टि का घटना बिंदु परिमित हो, विविक्त प्रतिदर्श समष्टि कहलाता है.

घटना (Event): प्रतिदर्श समष्टि के प्रत्येक उपसमुच्चय को घटना कहते है. इसे प्रायः E से व्यक्त किया जाता है.

जैसे;

• एक सिक्के की उछाल में S {H, T}
• यदि Head आने की घटना E हो, तो E = {H} ⊆ S
• यदि S प्रतिदर्श समष्टि हो, तो किसी घटना E की प्रायिकता P(E) = n(E)/n(S)
• जहाँ n(E) = समुच्चय E के अवयवों की संख्या
• n(E) = प्रतिदर्श समष्टि S के अवयवों की संख्या

सरल घटना (Elementary Event): प्रतिदर्श समष्टि का वह उपसमुच्चय, जिसमे केवल एक अवयव हो, वह सरल घटना कहलाता है.

असंभव घटना (Impossible Event): वैसी घटना जिसमे एक भी अवयव नही हो, वह असंभव घटना कहलाता है.

जैसे; पासे फेंककर H प्राप्त करने की घटना, एक असंभव घटना है. इसे Φ से व्यक्त किया जाता है.

घटना के सम्बन्ध में प्रयकिता की नियम

• गिनती का योग नियम

यदि E एक घटना है जो घटना E1 या E2 में से किसी एक के घटने से घटित होती हैं, तो

n(E) = n(E1) + n(E2) को गिनती का योग नियम कहते है.

• गिनती का गुणन नियम

यदि E एक घटना है, जो घटना E1 एवं E2 दोनों के एक साथ घटने से घटती हैं, तो

n(E) = n(E1) × n(E2)

• क्रमचय

यदि E कोई घटनाहै यह तभी घटित होती है, जब n विभिन्न वस्तुओं में r वस्तुएं सजाई जाती हैं.

n(E) = nPr = n!/(n – r)!

• संचय

घटना E तभी घटित होती हैं, जब n विभिन्न वस्तुओं में से r वस्तुएं चुनी जाती हैं।

n(E) = nCr = n!/r!( n – r)!

• प्रायिकता का सूत्र

यदि E = घटना और S प्रतिदर्श समष्टि, तो

P (E) = n(E)/n(S)

अर्थात, प्रायिकता = संभावित परिणामों की संख्या / कुल परिणामों की संख्या

जहाँ n(E) = E के अवयवों की संख्या और n(S) प्रतिदर्श समष्टि के अवयवों की संख्या है.

ताश से सम्बंधित महत्वपूर्ण तथ्य

• ताश की एक गद्दी में कुल पत्तों की संख्या 52 होती हैं.
• एक गद्दी में 26 लाल और 26 काले रंग के पत्ते होते हैं.
• 26 लाल रंग के पत्तों में 13 लाल पान और 13 ईंट के पत्ते होते हैं.
• 26 काले रंग के पत्तों में 13 काला पान और 13 चिड़िया के पत्ते होते हैं.
• ताश की गद्दी में कुल चार इक्के, प्रकार चार बादशाह, चार बेगम एवं चार गुलाम होते हैं.
• एक गद्दी में कुछ फेस कार्ड की संख्या 12 होती है.

प्रायिकता से संबंधित महत्वपूर्ण फार्मूला

• P(A) + P(A’) = 1, जहाँ A कोई घटना हैं तथा A’ इसकी पूरक घटना हैं.
• घटना के अनुकूल संयोगानुपात E = P(E) : P(E’)
• घटना के प्रतिकूल संयोगानुपात E = P(E’) : P(E)
• यदि घटना के अनुकूल संयोगानुपात = a : b तो P(E) =
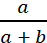
• यदि घटना E का प्रतिकूल संयोगानुपात = a : b तो P(E) =
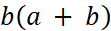
• P(E) + P(E’) = 1
• यदि किसी प्रतिदर्श समष्टि S में A, B तथा C तीन घटनाएं हो, तो

P(A∪B∪C) = P(A) + P(B) + P(C) – P(A∩B) – P(B∩C) – (A∩C) + P(A∩B∩C)

Prayikta प्रतियोगिता एग्जाम के लिए सर्वाधिक महत्वपूर्ण होता है. एग्जाम फार्मूला एवं ट्रिक्स का उपयोग करना बहुत आवश्यक होता है. इसलिए, यहाँ Prayikta सम्बंधित सभी आवश्यक फार्मूला का विवरण दिया गया है जो सरलता से प्रश्न हल करने में मदद करता है.

1. एक क्रिकेट मैच में, एक महिला बल्लेबाज खेली गई 30 गेंदों में 6 बार चौका मारती है। चौका न मारे जाने की प्रायिकता ज्ञात कीजिए।

हलः

बल्लेबाज द्वारा खेली गई गेंदों की संख्या = 30

गेंदों की संख्या जिन पर चौका मारा = 6

गेंदों की संख्या जिन पर चौका नहीं लगा = 30 – 6 = 24

P (चौका नहीं लगेगा)।

= गेंदों की संज्या जिन पर चौका नहीं लगा/उसके द्वारा खेली गई गेंदों की कुल संख्या

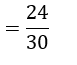
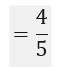
2. बच्चों वाले 1500 परिवारों का यादृच्छया चयन किया गया है। और निम्नलिखित आंकड़े लिख लिए गए हैं :

परिवार में लड़कियों की संख्या	परिवारों की संख्या
2 1 0	475 814 211

एक परिवार यादृच्छया चुना गया। प्रायिकता ज्ञात कीजिए कि उसमें

(i) दो लड़कियाँ हों (ii) एक लड़की हो (iii) कोई लड़की न हो।

साथ ही, यह भी जाँच कीजिए कि इन प्रायिकताओं का योगफल 1 है। या नहीं।

हलः

1) परिवारों की कुल संख्या = 1500

2 लड़कियों वाले परिवारों की संख्या = 475

P (दो लड़कियां)

= 2 लड़कियों वाले परिवारों की संख्या/परिवारों की कुल संख्या

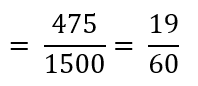
2) 1 लड़की वाले परिवारों की संख्या = 814

∴ P (1 लड़की)

= 1 लड़की वाले परिवारों की संख्या/परिवारों की कुल संख्या

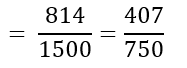
3) परिवारों की संख्या जिनकी कोई लड़की नहीं है।

= 211

∴ P (कोई लड़की नहीं)

= परिवारों की संज्या जिनकी कोई लड़की नहीं है।/परिवारों की कुल संख्या

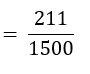
जाँच :

प्रायिकताओं का योग

अतः सभी तीन प्रायिकताओं का योगफल 1 है।

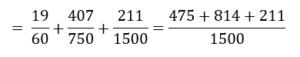
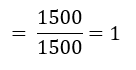
अतः सभी तीन प्रायिकताओं का योगफल 1 है।

3. तीन सिक्कों को एक साथ 200 बार उछाला गया है तथा इनमें विभिन्न परिणामों की बारंबारताएँ ये हैं :

परिणाम	बारंबारता
3 चित 2 चित 1 चित कोई भी चित नहीं	23 72 77 28

यदि तीनों सिक्कों को पुनः एक साथ उछाला जाए, तो दो चित आने की प्रायिकता ज्ञात कीजिए।

हलः

तीन सिक्कों को एक साथ जितनी बार उछाला गया = 200

2 चित आने की बारंबारता = 72

2 चित आने की प्रायिकता अर्थात् P (2 चित)

= 2 चित आने की बारंबारता/तीन सिक्कों को एक साथ जितनी बार उछाला गया

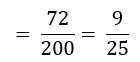
4. एक कंपनी ने यादृच्छया 2400 परिवार चुनकर एक घर की आय, स्तर और वाहनों की संख्या के बीच संबंध स्थापित करने के लिए उनका सर्वेक्षण किया। एकत्रित किए गए आंकड़े आगे सारणी में दिए गए हैं।

प्रति परिवार वाहनों की संख्या

मासिक आय (₹ में )	0	1	2	2 से अधिक
7000 से कम 7000-10000 10000-13000 13000-16000 16000 या इससे अधिक	10 0 1 2 1	160 305 535 469 579	25 27 29 59 82	0 2 1 25 88

मान लीजिए एक परिवार चुना गया है। प्रायिकता ज्ञात कीजिए कि चुने गए परिवार :

• की आय ₹ 10000-13000 प्रति माह है और उसके पास ठीक-ठीक दो वाहन हैं।
• की आय प्रति माह में ₹ 16000 या इससे अधिक है और उसके पास ठीक 1 वाहन है।
• की आय ₹ 7000 प्रति माह से कम है और उसके पास कोई वाहन नहीं है।
• की आय ₹ 13000-16000 प्रति माह है और उसके पास 2 से अधिक वाहन हैं।
• जिसके पास 1 से अधिक वाहन नहीं है।

हलः

कंपनी द्वारा सर्वेक्षण किए गए परिवारों की कुल संख्या = 2400

• ₹ 10,000 – ₹ 13000 प्रति माह आय वाले और ठीक-ठाक दो वाहन रखने वाले परिवारों की संख्या = 29

∴ P(₹ 10,000 – ₹ 13000 प्रति माह आय और ठीक-ठीक दो वाहन)

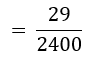
• ₹ 16000 या अधिक प्रति माह आय वाले और ठीक 1 वाहन रखने वाले परिवारों की संख्या = 579

∴ P(₹ 16000 या इससे अधिक प्रतिमाह आय और ठीक 1 वाहन)

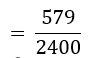
• ₹ 7000 प्रतिमाह से कम और कोई वाहन न रखने वाले परिवारों की संख्या = 10

∴ P (₹ 7000 से कम और कोई वाहन न रखने वाला परिवार)

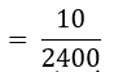
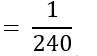
• ₹ 13000 – 16000 प्रति माह आय वाले और 2 से अधिक वाहन रखने वाले परिवारों की संख्या = 25

∴ P (₹ 13000 – 16000 आय और 2 से अधिक वाहन रखने वाले)

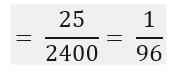
• परिवारों की संख्या जिसके पास 1 से अधिक वाहन नहीं हैं।

= कोई वाहन न रखने वाले परिवारों की संख्या + केवल 1 वाहन रखने वाले परिवारों की संख्या

= (10 + 0 + 1 + 2 + 1) + (160 + 305 + 535 + 469 + 579)

= 14 + 2048

= 2062

∴ P (एक परिवार जिसके पास 1 से अधिक वाहन नहीं हैं।

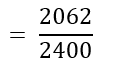
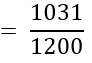
5. सांख्यिकी के बारे में विद्यार्थियों का मत जानने के लिए 200 विद्यार्थियों का सर्वेक्षण किया गया। प्राप्त आँकड़ों को नीचे दी गई सारणी में लिख लिया गया है :

मत	विद्यार्थियों की संख्या
पसंद करते हैं पसंद नहीं करते हैं	135 65

प्रायिकता ज्ञात कीजिए कि यादृच्छया चुना गया विद्यार्थी

• सांख्यिकी पसंद करता है।
• सांख्यिकी पसंद नहीं करता है।

हलः

सांख्यिकी के विद्यार्थियों की कुल संख्या जिन पर सर्वेक्षण किया गया = 200

1. विद्यार्थियों की संख्या जो सांख्यिकी को पसंद करते हैं।

= 135

∴ P (सांख्यिकी पसंद करता विद्यार्थी)

सांज्यिकी को पसंद करने वाले

= विद्यार्थियों की संख्या/विद्यार्थियों की कुल संख्या

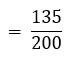
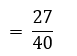
2. सांख्यिकी को पसंद न करने वाले विद्यार्थियों की संख्या = 65

∴ P (सांख्यिकी को पसंद न करने वाला विद्यार्थी)

सांज्यिकी को पसंद न करने वाले

= विद्यार्थियों की संख्या/विद्यार्थियों की कुल संख्या

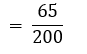
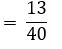
6. अपने विद्यालय के गेट के सामने से एक समय-अंतराल में गुजरने वाले दो पहिया, तीन पहिया और चार पहिया वाहनों की बारंबारता लिख लीजिए। आप द्वारा देखे गए वाहनों में से किसी एक वाहन का दो पहिया वाहन होने की प्रायिकता ज्ञात कीजिए।

हलः

मान लीजिए आपने विद्यालय के समय के बाद (3 p.m. से 3.30 p.m.) आधा घंटा विद्यालय के गेट के बाहर से गुजरने वाले वाहनों के प्रकार को देखा है।

मान लीजिए वाहनों की बारंबारता नीचे दी गई सारणी में दर्शाई गई है :

वाहन का प्रकार	वाहनों की बारंबारता
दो पाहिया तीन पहिया चार पहिया	125 45 30

इस समय अंतराल में गुजरने वाले वाहन का दो पहिया वाहन होने की प्रायिकता

समय अंतराल में देखे गए

= दो पहिया वाहनों की संख्या/वाहनों की कुल संख्या

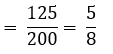
7. आप अपनी कक्षा के विद्यार्थियों से एक 3 अंक वाली संख्या लिखने को कहिए। आप कक्षा से एक विद्यार्थी को यादृच्छया चुन लीजिए। इस बात की प्रायिकता क्या होगी कि उसके द्वारा लिखी गई संख्या 3 से भाज्य है? याद रखिए कि कोई संख्या 3 से भाज्य होती है, यदि उसके अंकों का योग 3 से भाज्य हो।

हलः

मान लीजिए आप की कक्षा में विद्यार्थियों की संख्या 24.

मान लीजिए प्रत्येक विद्यार्थी द्वारा लिखी गई 3 अंक वाली संख्याएँ हैं : 837, 172, 643, 371, 124,512, 432, 948, 311, 252, 999, 557, 784, 928, 867, 798, 665, 245, 107, 463, 267, 523, 944, 314. 3 से विभाजित होने वाली संख्याएँ हैं : 837,432, 948, 252, 999, 867, 798 और 267

3 से विभाजित होने वाली 3 अंकों वाली संख्याओं की संख्या 8 है :

∴ P (3 अंकों वाली 3 से विभाजित संख्या)

3 से विभाजित होने वाली 3

= अंकों वाली संज्याओं की संज्या/कक्षा में विद्यार्थियों की कुल संज्या

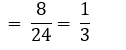
8. आटे की उन ग्यारह थैलियों में, जिन पर 5 किग्रा अंकित है, वास्तव में आटे के निम्नलिखित भार (किग्रा में ) हैं :

4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, 5.04, 5.07, 5.00. यादृच्छया चुनी गई एक थैली में 5 किग्रा से अधिक आटा होने की प्रायिकता क्या होगी ?

हलः

आटे की थैलियों की कुल संख्या = 11

5 किग्रा से अधिक आटे वाली थैलियों की संख्या = 7

P (5 किग्रा से अधिक आटा)

5 किग्रा से अधिक आटे वाली

= थैलियों की संख्या/थैलियों की कुल संख्या