पाठ 4, दो चरों वाले रैखिक समीकरण

 दो चरों वाले रैखिक समीकरण

एक समीकरण ऐसा कथन है जिसमें एक व्यंजक दूसरे व्यंजक के बराबर होता है। ax + by + c = 0, के रूप की समीकरण, जहाँ a, b और c वास्तविक संख्याएँ हैं, ताकि a ≠ 0 आरै b ≠ 0 हो, दो चरों में एक रैखिक समीकरण कहलाती है।

किसी रैखिक समीकरण के हल पर कोई प्रभाव नहीं पड़ता, जब

• समीकरण के दोनों पक्षों में एक ही संख्या जोड़ी जाए (या उनमें से एक ही संख्या घटाई जाए)।
• समीकरण के दोनों पक्षों को एक ही शून्येतर संख्या से गुणा किया (या भाग दिया) जाए।

रैखिक समीकरण के हल

दो चरों वाली एक रैखिक समीकरण के अपरिमित रूप से अनेक हल होते हैं। दो चरों वाली प्रत्येक रैखिक समीकरण का आलेख एक सरल रेखा होता है तथा इस आलेख (सरल रेखा) पर स्थित प्रत्येक बिंदु उस रैखिक समीकरण का एक हल निरूपित करता है। इस प्रकार, रैखिक समीकरण के प्रत्येक हल को समीकरण के आलेख पर एक अद्वितीय बिंदु द्वारा निरूपित कर सकते हैं। x = a और y = a के आलेख क्रमशः y-अक्ष और x-अक्ष के समांतर रेखाएँ हैं।

रैखिक समीकरण के सापेक्ष किसी बिंदु की स्थिति ज्ञात करना

किसी दिए हुए बिंदु की स्थिति क्या है इसको ज्ञात करने के लिए रैखिक समीकरण में x और y मान को रखते हैं अगर वह समीकरण को पूर्णतया संतुष्ट करता है तो बिंदु रेखा पर स्थित है अन्यथा नहीं तथा बिंदु की रेखा से निकटतम दूरी कितनी है इसे भी आसानी से ज्ञात किया जा सकता है एक उदाहरण के माध्यम से इसे समझने का प्रयास करते हैं।

हल सहित उदाहरण

उन बिंदुओं के निर्देशांक ज्ञात कीजिए जहाँ समीकरण 3x + 4y = 12 का आलेख x-अक्ष और y- अक्ष को काटता है।

हल:

रैखिक समीकरण 3x + 4y = 12 का आलेख x-अक्ष को उस बिंदु पर काटता है जहाँ y = 0 है।

रैखिक समीकरण में, y = 0 रखने पर, हमें 3x = 12, अर्थात् x = 4 प्राप्त होता है। इस प्रकार, वाँछित बिंदु (4, 0) है।

रैखिक समीकरण 3x + 4y = 12 का आलेख y- अक्ष को उस बिंदु पर काटता है, जहाँ x = 0 है। दी हुई समीकरण में, x = 0 रखने पर, हमें 4y = 12, अर्थात् y = 3 प्राप्त होता है। इस प्रकार, वाँछित बिंदु (0, 3) है।

अक्ष के सापेक्ष रेखा की स्थिति

• यदि कोई रेखा x-अक्ष पर है तो वहाँ y = 0 होगा और यदि रेखा y-अक्ष पर है तो x = 0 होगा।
• यदि कोई रेखा x-अक्ष के समान्तर है तो x के विभिन्न मानों के लिए y का मान निश्चित होगा और यदि रेखा y-अक्ष के समान्तर है तो y के विभिन्न मानों के लिए x का मान निश्चित होगा
• मूल बिंदु से होकर गुजरने वाली रेखा का समीकरण ax + by = 0 होता है।

हल सहित उदाहरण

रैखिक समीकरण x + y = 5 का आलेख उस रेखा को किस बिंदु पर काटता है जो y- अक्ष के समांतर है, मूलबिंदु से 2 मात्रक की दूरी पर है तथा x-अक्ष की धनात्मक दिशा में है।

हल:

उस रेखा पर स्थित बिंदुओं के निर्देशांक, जो y-अक्ष के समांतर हैं, मूलबिंदु से 2 मात्रक की दूरी पर हैं तथा x- अक्ष की धनात्मक दिशा में हैं, (2, a) के रूप के होंगे। समीकरण x + y = 5 में, x = 2 आरै y = a रखने पर, a = 3 प्राप्त होता है। इस प्रकार, वाँछित बिंदु (2, 3) है।

समीकरण 2x + 5y = 20 के आलेख पर वह बिंदु निर्धारित कीजिए जिसका x- निर्देशांक कोटि का 5/2 गुना है।

क्योंकि बिंदु का ग- निर्देशांक उसकी कोटि का गुना है, इसलिए x =  y है।

अब 2x + 5y = 20 में x =  y रखने पर, y = 2 प्राप्त होता है।

अतः x = 5 है, इसलिए वांछित बिंदु (5, 2) है।

दो चरों वाले रैखिक समीकरण के प्रयोग

रैखिक समीकरणों के उपयोग से संख्याओं, आयु, परिमापों तथा मुद्रा के रूप में प्रयोग होने वाले सिक्कों व नोटों पर आधारित अनेक प्रकार की समस्याएँ हल की जा सकती हैं।

रैखिक बहुपद घात

एक रैखिक बहुपद घात एक का बहुपद होता है, अर्थात, चर का उच्चतम घातांक एक होता है, जैसे: ax + by + c = 0 जिसमें a, b और c वास्तविक संख्याएं हैं तथा a ≠ 0 और b ≠ 0

रैखिक समीकरण के उपयोग वाले उदाहरण

किसी पिंड पर एक अचर बल लगाने पर, उसके द्वारा किया गया कार्य उस अचर बल और बल की दिशा में पिंड द्वारा चली गई दूरी के गुणनफल के बराबर होता है। अचर बल 3 मात्रक लेते हुए, इस तथ्य को एक रैखिक समीकरण के रूप में व्यक्त कीजिए तथा उसका आलेख खींचिए। किया गया कार्य कितना है, जब चली गई दूरी 2 मात्रक है।

उत्तर:

किया गया कार्य = (अचर बल) × (दूरी)

= 3 × (दूरी),

अर्थात्, y = 3x है, जहाँ y (मात्रक) किया गया कार्य है तथा x (मात्रक) चली गई दूरी है। क्योंकि x = 2 मात्रक ( दिया) है, अतः, किया गया कार्य = 6 मात्रक है।

हम देखते हैं कि x = 0, y = 0 इस समीकरण को संतुष्ट करता है तथा x = 1, y = 3 भी इस समीकरण को संतुष्ट करता है।

उदाहरण

उदाहरण 1. एक नोटबुक की कीमत एक कलम की कीमत से दो गुनी है। इस कथन को निरूपित करने के लिए दो चरों वाला एक रैखिक समीकरण लिखिए। (संकेत मान लीजिए, नोटबुक की कीमत x रु है और कलम की कीमत y रु है)।

हल:
माना पेन की कीमत  = y रुपया है
और नोटबुक की कीमत = x रुपया है
प्रश्नानुसार,
नोटबुक की कीमत = 2 (पेन की कीमत)
x = 2y
⇒ x – 2y = 0

उदाहरण 2. निम्नलिखित रैखिक समीकरणों को ax + by + c = 0  के रूप में व्यक्त कीजिए और प्रत्येक स्थिति में  a, b और c के मान बताइए:

• 2x + 3y = 9.35
• x – 5y – 10 = 0
• –2x + 3y = 6

हल:

• 2x + 3y = 9.35
  दिए गए समीकरण कोax + by + c = 0  के रूप में व्यक्त करने पर
  ⇒  2x + 3y – 9.35 =  0
  अत:   a = 2, b = 3, c = – 9.35

• x –5y – 10 = 0
  दिए गए समीकरण कोax + by + c = 0  के रूप में व्यक्त करने पर
  ⇒ x –5y – 10 = 0
  अत: , a = 1, b = -5, c = -10

• –2x + 3y = 6
  दिए गए समीकरण कोax + by + c = 0  के रूप में व्यक्त करने पर
  ⇒ –2x + 3y – 6 = 0
  अत:, a = – 2, b = 3, c = – 6

उदाहरण 3. निम्नलिखित विकल्पों में से कौन-सा विकल्प सत्य है, और क्यों?
y = 3x + 5 का

• एक अद्वितीय हल है,
• केवल दो हल है,
• अपरिमित रूप से अनेक हल हैं|

हल: अपरिमित रूप से अनेक हल हैं|

उदाहरण 4. निम्नलिखित समीकरणों में से प्रत्येक समीकरण के चार हल लिखिए:

• 2x + y = 7
• πx + y = 9
• x = 4y

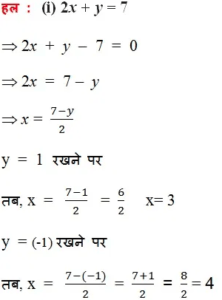
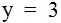
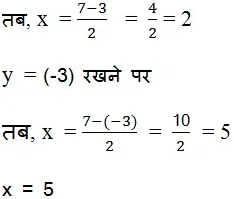
अत: x और y का दिए गए समीकरण के लिए चार हल निम्नलिखित है:

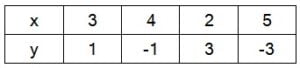
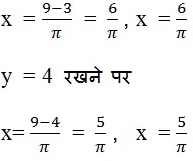
अत: x और y का दिए गए समीकरण के लिए चार हल निम्नलिखित है:

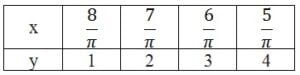
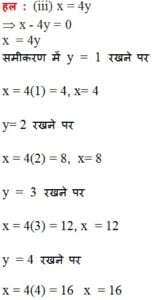
अत: x और y का दिए गए समीकरण के लिए चार हल निम्नलिखित है:

उदाहरण 5. दो चरों वाले निम्नलिखित रैखिक समीकरण का आलेख खींचिए:
3 = 2x + y

हल:

3 = 2x + y
⇒ y = 3 – 2x
समीकरण में x का मान 0, 1 और -1 रखने पर y का मान क्रमश: 3, 1 और  5 प्राप्त होता है

जिसकी सारणी निम्न है –

 

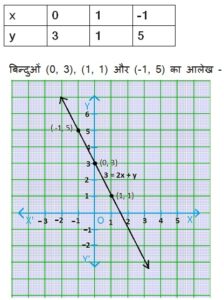
उदाहरण 6. अमरीका और कनाडा जैसे देशों में तापमान फारेनहाइट में मापा जाता है, जबकि भारत जैसे देशों में तापमान सेल्सियस में मापा जाता है। यहाँ फारेनहाइट को सेल्सियस में रूपांतरित करने वाला एक रैखिक समीकरण दिया गया है:

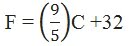
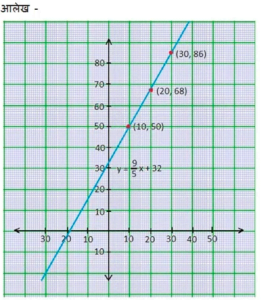
• सेल्सियस को x-अक्ष और फारेनहाइट को y-अक्ष मानकर ऊपर दिए गए रैखि समीकरण का आलेख खींचिए।
• यदि तापमान 30°C है, तो फारेनहाइट में तापमान क्या होगा?
• यदि तापमान 95°F है, तो सेल्सियस में तापमान क्या होगा?
• यदि तापमान 0°C है, तो फारेनहाइट में तापमान क्या होगा? और यदि तापमान 0°F है, तो सेल्सियस में तापमान क्या होगा?
• क्या ऐसा भी कोई तापमान है जो फारेनहाइट और सेल्सियस दोनों के लिए संख्यात्मकत: समान है? यदि हाँ, तो उसे ज्ञात कीजिए।

हल :

इसीप्रकार x का मान 20 और 30 रखने पर y का मान 68 और 86 प्राप्त होगा

जिसकी तालिका निम्न है|

(v) माना t वह तापमान है जो सेल्सियस और फारेनहाईट दोनों में संख्यात्मक रूप से समान है|

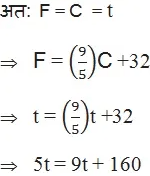
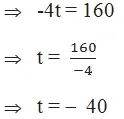
उदाहरण 7.

• एक चर वाले
• दो चर वाले

समीकरण के रूप में y = 3 का ज्यामितीय निरूपण कीजिए।
हल:

• एक चर वाले समीकरण के रूप में y = 3 का ज्यामितीय निरूपण:
  संख्या रेखा खींचिए और उस पर 0 के दायीं ओर तीसरा चिह्न चिह्नित कीजिए।

अतः y = 3 की संख्या- रेखा पर यही ज्यामितीय स्थिति है।

• दो चर वाले समीकरण के रूप में y = 3 को ज्यामितीय निरूपण:
  • वर्ग पत्रक (ग्राफ पेपर) पर X-अक्ष तथा Y-अक्ष खींचकर उन पर मापन चिह्न अंकित कीजिए।
  • Y-अक्ष पर +3 चिह्न से X-अक्ष के समान्तर रेखा AB खींचिए।

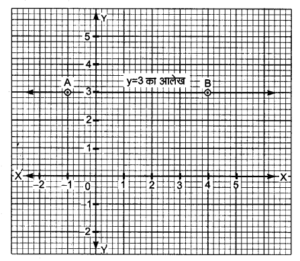
इस रेखा पर x ( भुज) के भिन्न-भिन्न मान वाले बिन्दुओं के लिए भी y (कोटि) का मान 3 स्थिर है।
ऋजु रेखा AB अभीष्ट आलेख है।

उदाहरण 8.

• एक चर वाले
• दो चर वाले

समीकरण के रूप में 2x + 9 = 0 का ज्यामितीय निरूपण कीजिए।
हल:

• एक चर वाले समीकरण के रूप में 2x + 9 = 0 का ज्यामितीय निरूपण:
  दिया हुआ समीकरण 2x + 9 = 0
  2x = -9
  x = -4
  संख्या-रेखा खींचिए। 0 के बायीं ओर -4 पर चिह्न लगाइए संख्या-रेखा पर 2x + 9 = 0 की यही स्थिति है।

• दो चर वाले समीकरण के रूप में 2x + 9 = 0 का ज्यामितीय निरूपण:
  • ग्राफ पेपर पर X-अक्ष तथा Y-अक्ष खींचकर उन पर मापक चिन्ह अंकित कीजिए।
  • X-अक्ष पर 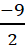 या -5 चिह्नित (अंकित) कीजिए और इससे Y-अक्ष के समान्तर रेखा AB खींचिए।

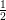इस रेखा पर स्थित सभी बिन्दुओं के लिए x = -4  होगा चाहे y का मान कुछ भी हो।
ऋजु रेखा AB अभीष्ट आलेख है।