पाठ 6, रेखाएँ और कोण
आधारभूत पद और परिभाषाएं
रेखाखण्ड–

किरण–
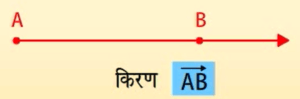
रेखा-

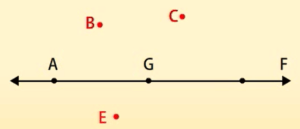
AGF संरेख बिन्दु हैं।
BCE असंरेख बिन्दु हैं।
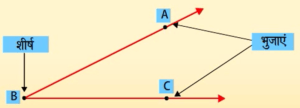
कोण
कोणों के प्रकार-
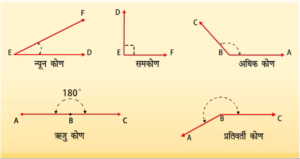
न्यूनकोण-
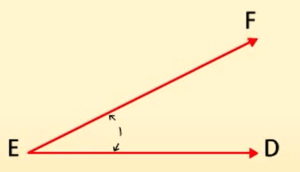
एक न्यूनकोण का माप 0° से 90° के बीच होता है।
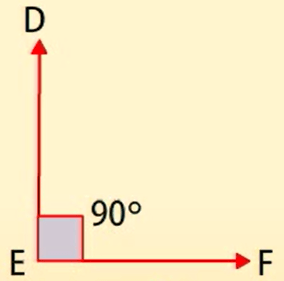
समकोण-
समकोण कोण ठीक 90° के बराबर होता है।
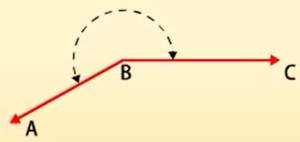
अधिक कोण-
अधिक कोण कोण 90° से ज्यादा और 180° से कम
ऋजु कोण-
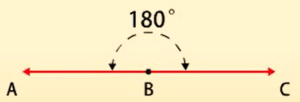
ऋजु कोण कोण 180° के बराबर
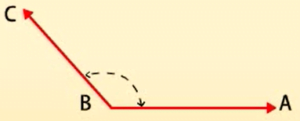
वृहत्तकोण-
कोण 180° से ज्यादा और 360° से कम
पूरक कोण–
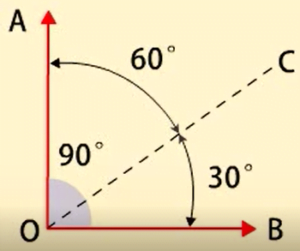
दो कोण जो एक साथ समकोण बनाते हैं, पूरक कोण कहलाते हैं।
सम्पूरक कोण-
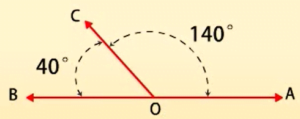
जिनका योग 180° हो
आसन्न कोण-
वैसे दो कोण जिसकी एक भुजा उभयनिस्ट हो और उनका एक ही शीर्ष हो आसन्न कोण कहलाता है।
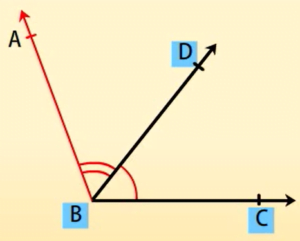
इन कोणों को आसन्न कोण कहते हैं।
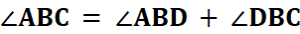
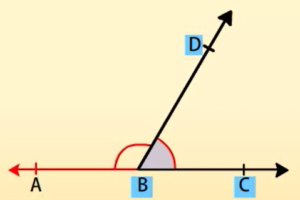
कोणों का रैखिक युग्म
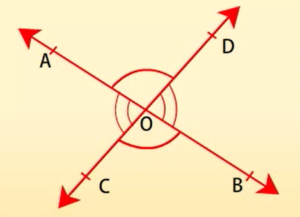
शीर्षाभिमुख कोण
प्रतिच्छेदी रेखाए और अप्रतिच्छेदी रेखाए
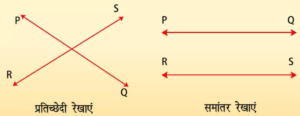
कोणो का युग्म
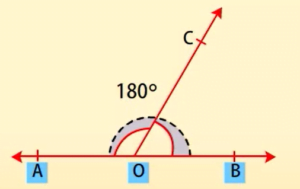
 AOC +
AOC +  BOC =
BOC =  AOB…….(i)
AOB…….(i)
 AOB = 180° …..(ii)
AOB = 180° …..(ii)
 AOC +
AOC +  BOC = 180°
BOC = 180°
अभिगृहीत I
अभिगृहीत 1: यदि एक किरण एक रेखा पर खड़ी हो, तो इस प्रकार बने दोनों आसन्न कोणों का योग 180° होता है।
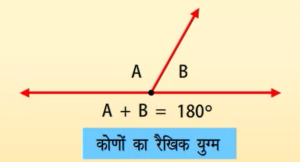
अभिगृहीत 2: यदि दो आसन्न कोणों का योग 180° हो तो एक किरण रेखा पर खड़ी होती है।
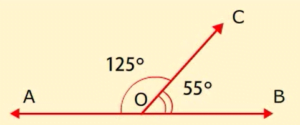
 AOC +
AOC +  COB
COB
125° + 55° = 180°
प्रमेय
यदि दो रेखाएं परस्पर प्रतिच्छेद करती हैं, तो शीर्षाभिमुख कोण बराबर होते हैं।
सिद्ध: यह दिया है कि दो रेखाएं एक-दूसरे को प्रतिच्छेद करती हैं। अतः, मान लीजिए कि AB और CDदो रेखाएं हैं जो परस्पर बिंदु पर प्रतिच्छेद करती हैं।
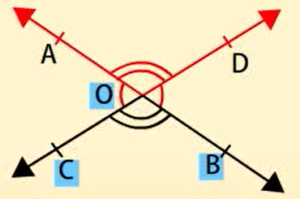
 AOC और
AOC और  BOD,
BOD,
 AOD और
AOD और  BOC शीर्षाभिमुख कोण हैं।
BOC शीर्षाभिमुख कोण हैं।
सिद्ध करे:  AOC =
AOC =  BOD
BOD
 AOD =
AOD =  BOC
BOC
यहां किरण OA रेखा CD पर खड़ी है।
अत:  AOC +
AOC +  AOD = 180° (रैखिक युग्म अभिगृहीत) …..(1)
AOD = 180° (रैखिक युग्म अभिगृहीत) …..(1)
इसी प्रकार  AOD +
AOD +  BOD = 180° …..(2)
BOD = 180° …..(2)
(1) और (2) से, हम निष्कर्ष निकाल सकते हैं कि
 AOC +
AOC +  AOD =
AOD =  AOD +
AOD +  BOD
BOD
 AOC =
AOC =  BOD
BOD
अतः  AOD =
AOD =  BOC
BOC
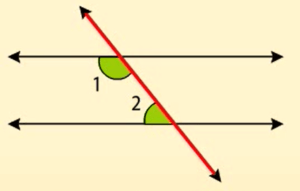
समांतर रेखाएं और तिर्यक रेखाएं
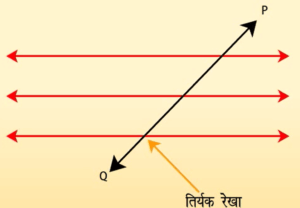
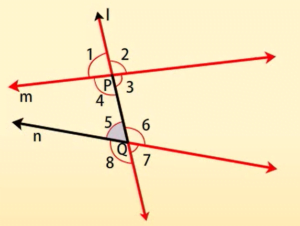
 1,
1,  2,
2,  7 और
7 और  8 बाह्य कोण कहलाते हैं।
8 बाह्य कोण कहलाते हैं।
 3,
3,  4,
4,  5 और
5 और  6 अंतः कोण कहलाते हैं।
6 अंतः कोण कहलाते हैं।
संगत कोण:
 1 और
1 और  5
5 2 और
2 और  6
6 4 और
4 और  8
8 3 और
3 और  7
7
एकांतर अंतः कोण:
 4 और
4 और  6
6 3 और
3 और  5
5
एकांतर बाह्य कोण :
 1 और
1 और  7
7 2 और
2 और  8
8
तिर्यक रेखा के एक ही ओर के अंतः कोण :
 4 और
4 और  5
5 3 और
3 और  6
6
तिर्यक रेखा के एक ही ओर के अंतः कोण क्रमागत अंतः कोण या संबंधित कोण या सह-अंतः कोण कहलाते हैं।
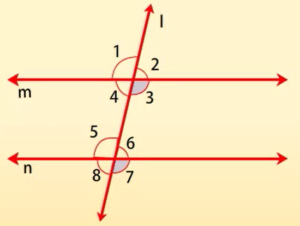
यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे, तो संगत कोणों का प्रत्येक युग्म बराबर होता है।
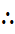
 1 =
1 =  5 ,
5 ,  2 =
2 =  6 ,
6 ,  4 =
4 =  8 ,
8 ,  3 =
3 =  7
7
अभिगृहीत 3: यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे, तो संगत कोणों का प्रत्येक युग्म बराबर होता है।
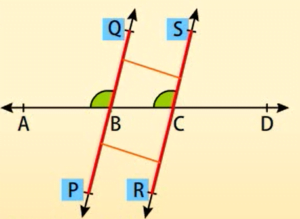
संगत कोण अभिगृहीत
विलोम: यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि संगत कोणों का एक युग्म बराबर हो, तो दोनों रेखाएं समांतर होती हैं।
अभिगृहीत 4: यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि संगत कोणों का एक युग्म बराबर हो, तो दोनों रेखाएं परस्पर समांतर होती हैं।
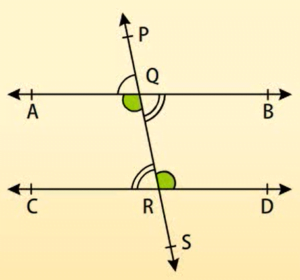
 PQA =
PQA =  QRC (संगत कोण अभिगृहीत) …(i)
QRC (संगत कोण अभिगृहीत) …(i)
 PQA =
PQA =  BOR ( शीर्षाभिमुख कोण) …(ii)
BOR ( शीर्षाभिमुख कोण) …(ii)
अतः (i) और (ii), से हम यह निष्कर्ष निकाल सकते हैं कि
 BQR =
BQR =  QRC
QRC
इसी प्रकार,  AQR =
AQR =  ORD
ORD
यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे, तो एकांतर अंतः कोणों का प्रत्येक युग्म बराबर होता है।
प्रमेय:
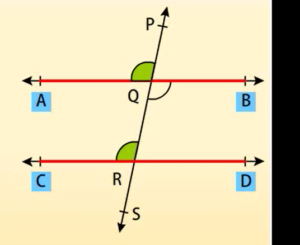
दिया है:  BQR =
BQR =  QRC
QRC
 BQR =
BQR =  PQA …(i)
PQA …(i)
(यशीर्षाभिमुख कोण)
 BOR =
BOR =  QRC …(ii) (दिया है)
QRC …(ii) (दिया है)
अतः (i) और (ii)
 PQA =
PQA =  QRC
QRC
(संगत कोण)
अतः AB || CD
(संगत कोण अभिगृहीत का विलोम)
अतः यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि एकांतर अंतः कोणों का एक युग्म बराबर है, तो दोनों रेखाएं परस्पर समांतर होती हैं।
प्रमेय:
यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे, तो तिर्यक रेखा के एक ही ओर के अंतः कोणों का प्रत्येक युग्म संपूरक होता है।
यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि तिर्यक रेखा के एक ही ओर के अंतः कोणों का एक युग्म संपूरक है, तो दोनों रेखाएं परस्पर समांतर होती हैं।
एक ही रेखा के समांतर रेखाएं
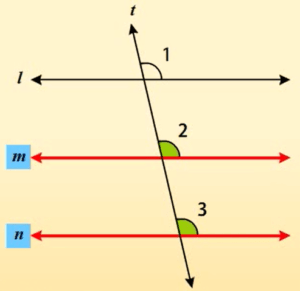
दिया है: रेखा m || रेखा l और रेखा n || रेखा l
 1 =
1 =  2 (संगत कोण अभिगृहीत)
2 (संगत कोण अभिगृहीत)
 1 =
1 =  3 (संगत कोण अभिगृहीत)
3 (संगत कोण अभिगृहीत)
 2 =
2 =  3
3
परन्तु  2 और
2 और  3 संगत कोण हैं और बराबर हैं।
3 संगत कोण हैं और बराबर हैं।
अतः रेखा m || रेखा n
(संगत कोण अभिगृहीत का विलोम)
प्रमेय:
वे रेखाएं जो एक ही रेखा के समांतर हों, परस्पर समांतर होती हैं।
उदाहरण:
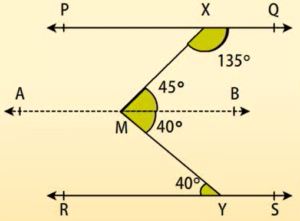
दिया है कि यदि PQ || RS,  MXQ = 135° और
MXQ = 135° और  MYR= 40°, तो
MYR= 40°, तो  XMY ज्ञात कीजिए।
XMY ज्ञात कीजिए।
AB || PQ, PQ || RS
= AB || RS
अब,  QXM +
QXM +  XMB = 180°
XMB = 180°
(AB || PQ, तिर्यक रेखा XM के एक ही ओर के अंतः कोण हैं।)
परन्तु  QXM = 135° अतः 135° +
QXM = 135° अतः 135° +  XMB = 180°
XMB = 180°
इसलिए,  XMB = 45° …(i)
XMB = 45° …(i)
अब,  BMY =
BMY =  MYR (AB || RS, एकांतर कोण)
MYR (AB || RS, एकांतर कोण)
इसलिए,  BMY = 40° …(ii)
BMY = 40° …(ii)
(i) और (ii), को जोड़ने पर हमें प्राप्त होता है
 XMB +
XMB +  BMY = 45° + 40°
BMY = 45° + 40°
इस प्रकार,  XMY = 85°
XMY = 85°
त्रिभुजों का कोण योग गुण
क्या आप बता सकते हैं त्रिभुज के सभी कोणों का योग कितना होता है?
त्रिभुज के कोणों का योग 180° होता है।
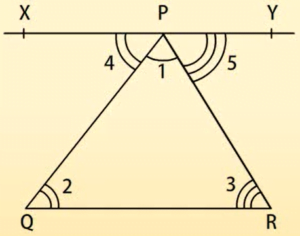
सिद्ध करना है कि:  1 +
1 +  2 +
2 +  3 = 180°
3 = 180°
अब XPY एक रेखा है।
अतः  4 +
4 +  1 +
1 +  5 = 180° …(i)
5 = 180° …(i)
परन्तु XPY II QR और PQ, PR तिर्यक रेखाएं हैं।
इसलिए,  4 =
4 =  2 और
2 और  5 =
5 =  3
3
(एकांतर कोणों के युग्म)
अब  4 और
4 और  5 के मान (i), रखने पर
5 के मान (i), रखने पर
 2 +
2 +  1 +
1 +  3 = 180°
3 = 180°
या  1 +
1 +  2 +
2 +  3 = 180°
3 = 180°
प्रमेय:
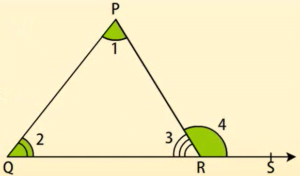
 3 +
3 +  4 = 180° …(i) (कोणों का रैखिक युग्म)
4 = 180° …(i) (कोणों का रैखिक युग्म)
21+22+ 23= 180°…(ii)
(त्रिभुज के सभी कोणों का योग)
(i) और (ii), के आधार पर हम कह सकते हैं।
 4 =
4 =  1 +
1 +  2
2
यदि एक त्रिभुज की एक भुजा बढ़ाई जाए, तो इस प्रकार बना बहिष्कोण दोनों अंतः अभिमुख (विपरीत) कोणों के योग के बराबर होता है।
इस प्रमेय से यह स्पष्ट है कि किसी त्रिभुज का एक बहिष्कोण अपने दोनों अंतः अभिमुख कोणों में से प्रत्येक से बड़ा होता है।
उदाहरण: यदि QT 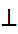 PR ,
PR ,  TOR = 40° और
TOR = 40° और  SPR = 30°, तो x और y ज्ञात कीजिए।
SPR = 30°, तो x और y ज्ञात कीजिए।
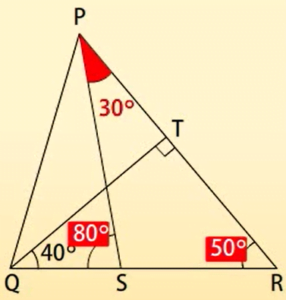
हल:  TOR में,
TOR में,
90° + 40° + x = 180°
(त्रिभुजों के कोण योग गुण के कारण)
अतः x = 50°
साथ ही, y =  SPR + x (बहिष्कोण गुण)
SPR + x (बहिष्कोण गुण)
अतः y = 30° + 50° = 80°
- एकांतर अंतः कोण, एकांतर वाह्य कोण, संगत कोण और तिर्यक रेखा के एक ही ओर के एकांतर कोण विभिन्न कोणों के नाम हैं जो रेखाओं के प्रतिच्छेद करने पर बनते हैं। इन नामों का प्रयोग तब करते हैं जब रेखाएं समांतर होती हैं और जब वे समांतर नहीं होती हैं।
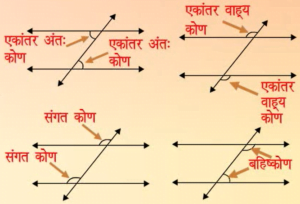
- एकांतर वाहय कोण
- संगत कोण
- संगत कोण
- बहिष्कोण
सारांश
- यदि एक किरण एक रेखा पर खड़ी हो तो इस प्रकार बने आसन्न कोणों का योग 180° होता है और इसका विलोम भी सत्य है। इस गुण को रैखिक युग्म अभिगृहीत कहते हैं।
- यदि दो रेखाएं परस्पर प्रतिच्छेद करती हैं तो उनके शीर्षाभिमुख कोण बराबर होते हैं।
- यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे तो
- (क) संगत कोणों का प्रत्येक युग्म बराबर होता है।
- (ख) एकांतर अंतः कोणों का प्रत्येक युग्म बराबर होता है।
- (ग) तिर्यक रेखा के एक ही ओर के अंतः कोणों का प्रत्येक युग्म संपूरक होता है।
- यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि या तो,
- (क) संगत कोणों का कोई युग्म बराबर हो या
- (ख) एकांतर अंतः कोणों का कोई युग्म बराबर हो या
- (ग) तिर्यक रेखा के एक ही ओर के अंतः कोणों का कोई एक युग्म संपूरक हो, तो ये दोनों रेखाएं समांतर होती हैं।
Comments are closed