पाठ 8, चतुर्भुज
चतुर्भुजों का परिचय
एक चतुर्भुज की चार भुजाएँ, चार कोण और चार शीर्ष होते हैं। चतुर्भुज ABCD में, AB, BC, CD और DA चार भुजाएँ हैं: A, B, C और D चार शीर्ष हैं तथा ∠A, ∠B, ∠C और ∠D शीर्षों पर बने चार कोण हैं।
विकर्ण
अब सम्मुख शीर्षों A और C तथा B और D को जोडि़ए। AC और BD चतुर्भुज ABCD के दो विकर्ण कहलाते हैं।
चतुर्भुज का कोण योग गुण
चतुर्भुज के कोणों का योग 360⁰ होता है। हम इसकी जाँच चतुर्भुज का एक विकर्ण खींच कर उसे दो त्रिभुजों में विभाजित करके कर सकते हैं।
मान लीजिए ABCD एक चतुर्भुज है और AC उसका एक विकर्ण ह ∆ADC के कोणों का क्या योग है?
हम जानते हैं कि
∠DAC + ∠ACD + ∠D = 180° (1)
इसी प्रकार ∆ ABC में
∠CAB + ∠ACB + ∠B = 180° (2)
(1) और (2) को जोड़ने पर
∠DAC + ∠ACD + ∠D + ∠CAB + ∠ACB + ∠B = 180° + 180° = 360°
अर्थात् चतुर्भुज के कोणों का योग 360° होता है।
चतुर्भुज के प्रकार
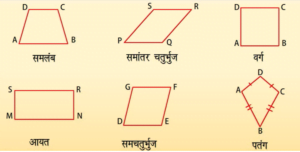
आकर के आधार पर चतुर्भुज विभिन्न प्रकार के होते हैं:
वर्ग चार भुजाओं से घिरी वह आकृति जिसकी चारो भुजाएँ बराबर हों तथा प्रत्येक कोण समकोण अर्थात 90° का हो, उसे वर्ग कहते हैं।
- आयत
- समचतुर्भुज
- समान्तर चतुर्भुज
- विषमकोण समचतुर्भुज
- समलम्ब चतुर्भुज
- चक्रीय चतुर्भुज
- पतंगाकार चतुर्भुज
वर्ग और आयत
वर्ग
- वर्ग चार भुजाओं से घिरी वह आकृति जिसकी चारो भुजाएँ बराबर हों तथा प्रत्येक कोण समकोण अर्थात 90° का हो, उसे वर्ग कहते हैं।
आयत
- ऐसा चतुर्भुज जिसके चारों अन्तःकोण समकोण (= 90° के) हों उसे आयत कहते हैं। आयत एक ऐसा चतुर्भुज है जिसकी आमने सामने की भुजाएं समांतर और बराबर होती है, “आयत” कहलाता है।
कुछ विशेष चतुर्भुज
समचतुर्भुज
- वह समांतर चतुर्भुज जिसकी चारों भुजाएँ बराबर हों।
समान्तर चतुर्भुज
- जिस चतुर्भुज की आमने-सामने की भुजाएँ समांतर तथा समान होती है उसे समान्तर चतुर्भुज कहते हैं।
विषमकोण समचतुर्भुज
- वह समान्तर चतुर्भुज, जिसकी चारों भुजाएँ बराबर होती हैं, किन्तु कोई कोण समकोण अर्थात् 90º का नहीं होता है, विषमकोण समचतुर्भुज कहलाता है।
चतुर्भुजों की परिभाषा
समलम्ब चतुर्भुज
- एक ऐसा चतुर्भुज जिसकी भुजाओं का एक युग्म समान्तर हो समलम्ब चतुर्भुज कहलाता हैं।
चक्रीय चतुर्भुज
- चक्रीय चतुर्भुज ऐसे चतुर्भुज को कहते हैं जिसके चारो शीर्ष किसी वृत्त की परिधि पर स्थित हों। किसी चक्रीय चतुर्भुज के आमने-सामने के कोणों का योग 180° होता है।
पतंगाकार चतुर्भुज
- पतंगाकार में आसन्न भुजाओं के दो युग्म बराबर लम्बाई के होते हैं। अर्थात एक विकर्ण, चतुर्भुज को दो सर्वांगसम त्रिभुजों में विभाजित करता हैं। इसलिए समान भुजाओं के दो युग्मों के बीच के कोण बराबर होते हैं। और दोनों विकर्ण एक दूसरे के लम्बवत होते हैं।
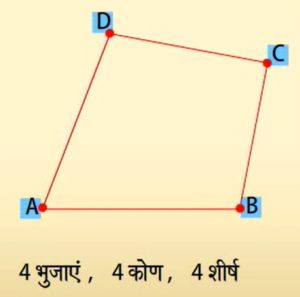
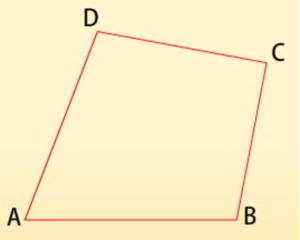
AB, BC, CD और DA चार भुजाएं हैं।
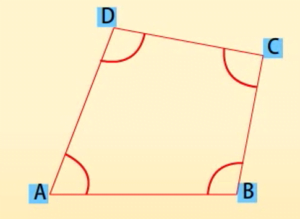
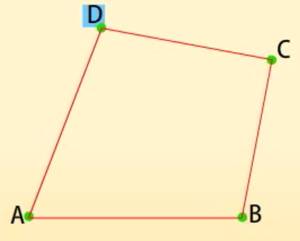
A, B, C और D चार शीर्ष हैं।
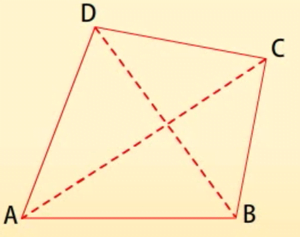
AC और BD विकर्ण हैं।
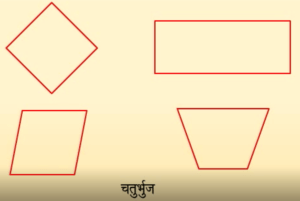
चतुर्भुज का कोण योग गुण
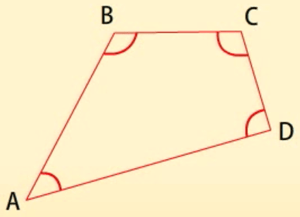
चतुर्भुज के सभी कोणों का योग 360 डिग्री होता है।
AC विकर्ण हैं
ABC और ADC दो त्रिभुज हैं।
त्रिभुज के सभी कोणों का योग 180 डिग्री होता है।
त्रिभुज ABC,  BAC +
BAC +  ACB +
ACB +  ABC = 180O ………(i).
ABC = 180O ………(i).
त्रिभुज ADC,  CAD +
CAD +  ACD +
ACD +  ADC = 180O ………(ii)
ADC = 180O ………(ii)
अब (i) और (ii) को योग करने पर हमें प्राप्त हुआ,
 BAC +
BAC +  ACB +
ACB +  B +
B +  CAD +
CAD +  ACD +
ACD +  D = 180O + 180O = 360O
D = 180O + 180O = 360O
साथ ही,  BAC +
BAC +  CAD =
CAD =  A और
A और  ACB +
ACB +  ACD =
ACD =  C
C
अतः  A +
A +  D +
D +  B +
B +  C = 360O
C = 360O
या  A +
A +  B +
B +  C +
C +  D = 360O
D = 360O
यानी चतुर्भुज के चारों कोणों का योग 360O होता है।
चतुर्भुज के प्रकार-I
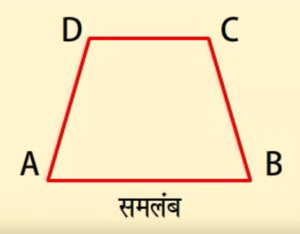
एक चतुर्भुज समलम्ब होता है यदि इसके सम्मुख भुजाओं का एक युग्म समांतर हो।
यहां, सम्मुख भुजाएं AB और CD समांतर हैं।
अतः ABCD एक समलम्ब है।
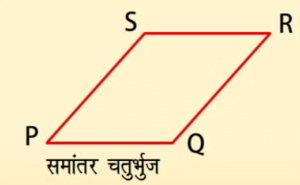
चतुर्भुज जब सम्मुख भुजाओं के दोनों युग्म समांतर हों तो ऐसा चतुर्भुज समांतर चतुर्भुज कहलाता है।
यहां सम्मुख भुजाएं PS और QR समांतर हैं।
तथा SR और PQ समांतर हैं।
अतः PORS एक समांतर चतुर्भुज है।
चतुर्भुज के प्रकार-II
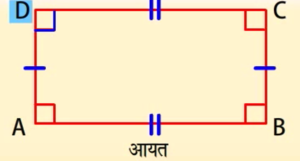
आयत में सम्मुख भुजाएं परस्पर समांतर होती हैं और लम्बाई में बराबर होती हैं। और सभी कोण 90 डिग्री के होते हैं।
AB II CD, AD II BC
 A,
A,  B,
B,  C और
C और  D = 90°
D = 90°
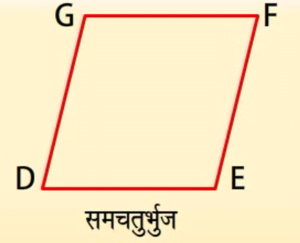
समचतुर्भुज समचतुर्भुज एक ऐसा चतुर्भुज है जिसकी सभी भुजाओं की लम्बाई बराबर हो।
DE, EE, FG और GD लम्बाई में बराबर हैं।
DEFG एक समचतुर्भुज है।
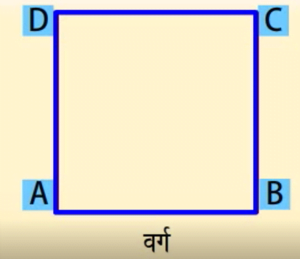
एक वर्ग जिसकी सभी भुजाएं बराबर होती हैं।
ABCD एक वर्ग है।
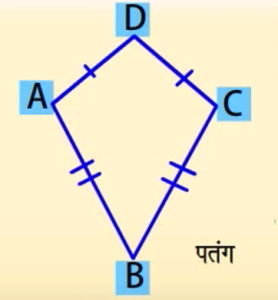
किसी पतंग की आसन्न भुजाएं बराबर होती हैं।
AD = DC तथा AB = BC
अतः ABCD एक पतंग है।
समांतर चतुर्भुज के गुण- I
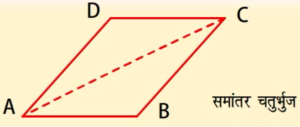
एक समांतर चतुर्भुज का एक विकर्ण इसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
सिद्ध करना है: 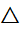 ABC और
ABC और 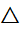 CDA सर्वांगसम हैं।
CDA सर्वांगसम हैं।
BC | | AD और AC एक तिर्यक रेखा है।
इसलिए,  BCA =
BCA =  DAC (क्योंकि ये एकांतर कोणों का युग्म है।)
DAC (क्योंकि ये एकांतर कोणों का युग्म है।)
AB | | DC और AC एक तिर्यक रेखा है।
इसलिए,  BAC =
BAC =  DCA (क्योंकि ये एकांतर कोणों का युग्म है।), और AC = CA (उभयनिष्ठ)
DCA (क्योंकि ये एकांतर कोणों का युग्म है।), और AC = CA (उभयनिष्ठ)
अतः 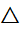 ABC = CDA (ASA नियम के प्रयोग से)
ABC = CDA (ASA नियम के प्रयोग से)
विकर्ण AC, समांतर चतुर्भुज ABCD को दो सर्वांगसम त्रिभुजों, त्रिभुज ABC और त्रिभुज CDA में विभाजित करती है।
समांतर चतुर्भुज के गुण-॥
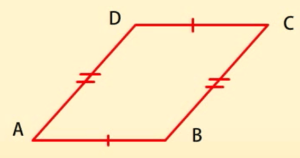
यदि हम समांतर चतुर्भुज ABCD की सम्मुख भुजाओं को मापेंगे तो हम देखेंगे कि
AB = DC और AD = BC
एक समांतर चतुर्भुज में सम्मुख भुजाएं बराबर होती हैं।
यदि एक चतुर्भुज समांतर चतुर्भुज है तो इसके सम्मुख भुजाओं का युग्म बराबर होता है।
विपरीतः यदि एक चतुर्भज के विपरीत पक्षों की प्रत्येक जोड़ी भुजा बराबर है, तो यह एक समांतर चतुर्भुज है।
दिया है: एक चतुर्भुज ABCD, AB = CD और AD = BC.
सिद्ध करना है: ABCD समांतर चतुर्भुज है।
AB = CD (दिया है), और AD = BC (दिया है), AC = AC (उभयनिष्ठ)
इसलिए नियम SSS से
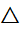 ABC
ABC 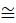
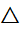 CDA तथा
CDA तथा
 1 =
1 =  2,
2,  3 =
3 =  4 (क्योंकि सर्वांगसम त्रिभुज के संगत भाग परस्पर सर्वांगसम होते हैं।)
4 (क्योंकि सर्वांगसम त्रिभुज के संगत भाग परस्पर सर्वांगसम होते हैं।)
AB II CD और AD II BC (एकांतर अंतः कोणों के प्रमेय का विलोम प्रयोग करके)। इस प्रकार ABCD एक समांतर चतुर्भुज है।
समांतर चतुर्भुज के गुण-III
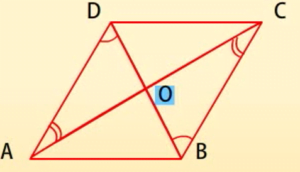
प्रमेय: एक समांतर चतुर्भुज में सम्मुख कोण बराबर होते हैं।
विलोमः यदि एक चतुर्भुज में सम्मुख कोणो का प्रत्येक युग्म परस्पर बराबर हों तो वह चतुर्भुज समांतर चतुर्भुज होता है।
यदि हम लम्बाईयां OA, OB, OC और OD मापें तो हम देखेंगे कि OA = OC और OB = OD है। O दोनों विकर्णों का एक मध्य-बिन्दु है।
समांतर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
समांतर चतुर्भुज के गुण- IV
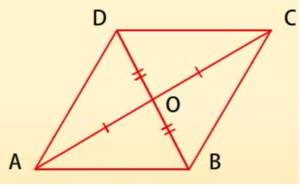
चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
विलोमः यदि किसी चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं तो यह एक समांतर चतुर्भुज है।
दिया है: OA = OC और OB = OD
 AOB =
AOB =  COD (शीर्ष कोण)
COD (शीर्ष कोण)
 AOD =
AOD =  BOC (शीर्ष कोण)
BOC (शीर्ष कोण)
 BDC
BDC 
 BAD (SAS नियम द्वारा)
BAD (SAS नियम द्वारा)
 BDC =
BDC =  ABD (सर्वांगसम त्रिभुज के संगत भाग सर्वांगसम होते, है।
ABD (सर्वांगसम त्रिभुज के संगत भाग सर्वांगसम होते, है।
इसी प्रकार  ADB
ADB 
 CBD इससे हमें, प्राप्त हुआ AB || CD (एकांतर अंतः कोणों के गुण के विलोम का प्रयोग करते हुए)
CBD इससे हमें, प्राप्त हुआ AB || CD (एकांतर अंतः कोणों के गुण के विलोम का प्रयोग करते हुए)
इसी प्रकार, BC || AD अतः ABCD एक समांतर चतुर्भुज है।
समचतुर्भुज के विकर्ण-
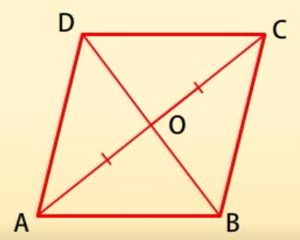
समचतुर्भुज के विकर्ण परस्पर लम्ब होते हैं।
हम जानते हैं कि AB = BC = CD = DA (समचतुर्भुज की सभी भुजाएं परस्पर बराबर होती हैं।)
अब 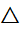 AOD और
AOD और 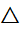 COD, OA = OC (क्योंकि समांतर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।)
COD, OA = OC (क्योंकि समांतर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।)
OD = OD (उभयनिष्ठ)
AD = CD (समचतुर्भुज की भुजाएं)
इसलिए, 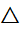 AOD
AOD 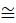
 COD (SSS नियम से)
COD (SSS नियम से)
 AOD =
AOD =  COD (CPCTC)
COD (CPCTC)
किन्तु  AOD +
AOD +  COD = 180° (क्योंकि ये कोणों के रैखिक युग्म हैं।)
COD = 180° (क्योंकि ये कोणों के रैखिक युग्म हैं।)
अतः 2  AOD = 180° या,
AOD = 180° या,  AOD = 90°
AOD = 90°
अतः समचतुर्भुज के विकर्ण परस्पर लम्ब होते हैं।
उदाहरण
सिद्ध कीजिए कि समांतर चतुर्भुज के कोणों के समद्विभाजक एक आयत का निर्माण करते हैं।
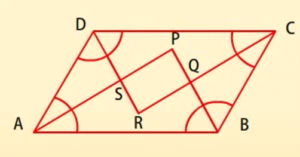
माना ABCD एक समांतर चतुर्भुज है।
मान लीजिए कि  A और
A और  B, के समद्विभाजक का प्रतिच्छेद बिन्दु P है।
B, के समद्विभाजक का प्रतिच्छेद बिन्दु P है।
 B और
B और  C के समद्विभाजक का प्रतिच्छेद बिन्दु Q है।
C के समद्विभाजक का प्रतिच्छेद बिन्दु Q है।
 C और
C और  D के समद्विभाजक का प्रतिच्छेद बिन्दु R है।
D के समद्विभाजक का प्रतिच्छेद बिन्दु R है।
 D और
D और  A के समद्विभाजक का प्रतिच्छेद बिन्दु S है।
A के समद्विभाजक का प्रतिच्छेद बिन्दु S है।
हम त्रिभुज ASD, में देख सकते हैं कि DS  D को और AS
D को और AS  A को समद्विभाजित करता है,
A को समद्विभाजित करता है,
 DAS +
DAS +  ADS =
ADS = 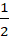
 A +
A + 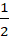 +
+  D
D
= 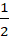 (
(  A +
A +  D)
D)
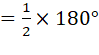 (
( A और
A और  D तिर्यक के एक ही ओर के एकांतर कोण हैं।)
D तिर्यक के एक ही ओर के एकांतर कोण हैं।)
इसलिए हम पाते हैं कि  DAS +
DAS +  ADS = 90O
ADS = 90O
साथ ही,  DAS +
DAS +  ADS +
ADS +  DSA = 180° (त्रिभुज का कोण योग गुण)
DSA = 180° (त्रिभुज का कोण योग गुण)
या, 90° +  DSA = 180°
DSA = 180°
या,  DSA = 90o
DSA = 90o
अतः  PSR = 90° (
PSR = 90° (  DSA का शीर्षाभिमुख कोण)।
DSA का शीर्षाभिमुख कोण)।
इसी प्रकार हम दिखा सकते हैं कि
 APB = 90° या,
APB = 90° या,  SPQ = 90
SPQ = 90
और  PQR = 90° और
PQR = 90° और  SRQ = 90°
SRQ = 90°
 PSR =
PSR =  POR = 90° और
POR = 90° और  SPQ =
SPQ =  SRQ = 90°
SRQ = 90°
अतः PORS एक समांतर चतुर्भुज है जिसमें कम से कम एक कोण 90° का है और इसलिए PORS एक आयत है।
किसी चतुर्भुज के समांतर चतुर्भुज होने के लिए प्रतिबन्ध-
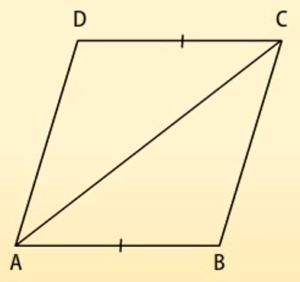
कोई चतुर्भुज एक समांतर चतुर्भुज होता है, यदि उसकी सम्मुख भुजाओं का एक युग्म बराबर हो और समांतर हो।
दिया है: AB = CD और AB || CD
सिद्ध कीजिए: ABCD एक समांतर चतुर्भुज है।
चूंकि AB = CD (दिया है)
AC = AC (उभयनिष्ठ)
 BAC =
BAC =  ACD (AB II CD)
ACD (AB II CD)
इसलिए SAS सर्वांगसम नियम से
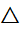 ABC
ABC 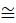
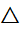 CDA
CDA
अतः  CAD
CAD 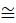
 ACB (CPCTC)
ACB (CPCTC)
इसलिए CB II AD (एकांतर अंतः कोण प्रमेय)
अतः ABCD एक समांतर चतुर्भुज है।
उदाहरण
यदि ABCD एक समांतर चतुर्भुज है जिसमें P और Q सम्मुख भुजाओं AB और CD के मध्य-बिन्दु हैं। AQ, DP को S पर प्रतिच्छेद करता है और BQ, CP को R पर प्रतिच्छेद करता है।
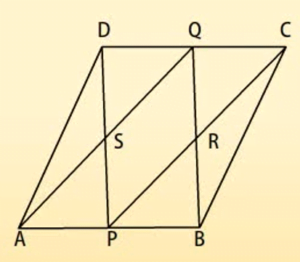
दर्शाइए किः DPBQ एक समांतर चतुर्भुज है।
हल: एक समांतर चतुर्भुज DPBQ में
DQ || PB (क्योंकि DC || AB) …(1)
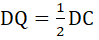 (दिया है)
(दिया है)
और 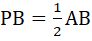 (दिया है)
(दिया है)
साथ ही, AB = CD (ABCD एक समांतर चतुर्भुज है।)
अतः, DQ = PB …(2)
अतः (1) और (2) से हम प्राप्त करते हैं कि DPBQ एक समांतर चतुर्भुज है।
मध्य बिन्दु प्रमेय-
मध्य बिन्दु प्रमेय: किसी त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समांतर होता है।
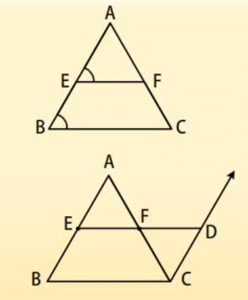
सिद्ध करना है: EF || Bc
त्रिभुज AEF और त्रिभुज CDF की तुलना करने पर,
 EAF =
EAF =  FCD (एकांतर अंतः कोण हैं।)
FCD (एकांतर अंतः कोण हैं।)
AF = FC (F एक मध्य-बिन्दु है।)
 AFE =
AFE =  CFD (दोनों शीर्षाभिमुख कोण हैं।)
CFD (दोनों शीर्षाभिमुख कोण हैं।)
इसलिए ASA सर्वांगसमता नियम से,
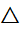 AEF
AEF 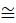
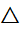 CDF
CDF
अतः EF = DF और AE = DC (CPCTC)
इसलिए BE = AE = DC
इसलिए BCDE एक समांतर चतुर्भुज है।
यह दिया है EF || BC
यह सिद्ध हुआ।
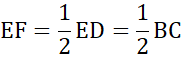
मध्य-बिन्दु प्रमेय का विलोम
किसी त्रिभुज की एक भुजा के मध्य-बिन्दु से दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
यहां E, AB का एक मध्य-बिन्दु है। रेखा i, E से होकर गुज़रती है और BC के समांतर है तथा CM || BA
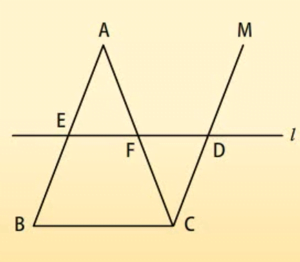
सिद्ध कीजिए: AF = CF
त्रिभुज AEF और CDF की सर्वांगसमता के प्रयोग से AF = FC के (CPCTC)
क्या आप जानते हैं-
- एक वर्ग एक आयत और एक समचतुर्भुज होता है।
- एक समांतर चतुर्भुज एक समलम्ब होता है।
- एक पतंग एक समांतर चतुर्भुज नहीं होती।
- एक समलम्ब एक समांतर चतुर्भुज नहीं होता।
- एक आयत या एक समचतुर्भुज एक वर्ग नहीं होता।
सारांश-
आइये हमने जो कुछ सीखा है, उसे संक्षेप में दोहराएं।
- चतुर्भुज के कोणों का योग 360 होता है।
- एक समांतर चतुर्भुज का विकर्ण इसको दो सर्वांगसम त्रिभुजों में विभाजित करता है।
- एक समांतर चतुर्भुज में-
- सम्मुख भुजाएं बराबर होती हैं।
- सम्मुख कोण बराबर होते हैं।
- विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
- किसी आयत के विकर्ण एक दूसरे को समद्विभाजित करते हैं और बराबर होते हैं।
- समचतुर्भुज के विकर्ण एक दूसरे को समकोण पर समद्विभाजित करते हैं।
सारांश-
आइये हमने जो कुछ सीखा है, उसे संक्षेप में दोहराएं।
- एक वर्ग का विकर्ण एक दूसरे को समकोण पर समद्विभाजित करते हैं। और बराबर होते हैं।
- त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समांतर और उसका आधा होता है।
- त्रिभुज की किसी एक भुजा के मध्य-बिन्दु से होकर जानी वाली तथा किसी अन्य भुजा के समांतर रेखा तीसरी भुजा को समद्विभाजित करती है।
- किसी चतुर्भुज के मध्य-बिन्दुओं को मिलाने से बनने वाला चतुर्भुज एक समांतर चतुर्भुज होता है।
Comments are closed