पाठ 8 गति
परिचय – गति (भौतिकी)
गति
गति (Motion): जब कोई वस्तु समय के साथ अपनी स्थिति में भी परिवर्तन करती है तो कहा जाता है कि वस्तु की गति में है |
हमारे आस-पास गतिशील वस्तुओं के बहुत से उदाहरण है |
जैसे – उड़ते हुए पक्षियों की गति, कार कि गति, धमनियों एवं शिराओं में रक्त की गति, दौड़ते हुए बालक की गति |
मूल-बिंदु(Origin): किसी वस्तु की स्थिति को बताने के लिए हमें एक निर्देश बिंदु कि आवश्यकता होती है, जिसे मूल बिंदु कहते हैं |
जैसे – कोई आम बोल-चाल कि भाषा में कहता है की इस चौराहे से रेलवे स्टेशन 20 किलोमीटर उत्तर में हैं |
तो यहाँ चौराहा मूल बिंदु है जो रेलवे स्टेशन की स्थिति को बता रहा है |.
दुरी (Distance): किसी वस्तु द्वारा किसी समय अन्तराल में तय की गए मार्ग कि लम्बाई को उस वस्तु द्वारा चली गयी दुरी कहते है |
विस्थापन (Displacement): किसी वस्तु के प्रारंभिक स्थिति तथा अंतिम स्थिति के बीच के न्यूनतम दुरी को वस्तु का विस्थापन कहते हैं |
परिमाण (Magnitiude): किसी भौतिक राशि के संख्यात्मक मान को इसका परिमाण कहते है |
सदिश एवं अदिश राशि
- सदिश राशि (Vector Quantity): वह भौतिक राशि जिसके परिमाण (maginitide) एवं दिशा (direction) दोनों होते हैं | उसे सदिश राशि कहते हैं | उदाहरण: भार, विद्युत आवेश, वेग, बल, संवेग, विस्थापन आदि |
- अदिश राशि (Scalar Quantity): वह भौतिक राशि जिसके केवल परिमाण () होता है दिशा नहीं होता है उसे अदिश राशि कहलाती है | उदाहरण: भार , समय. क्षेत्रफल, आयतन, चाल, दुरी, ताप, घनत्व आदि |
सरल रेखीय गति
जब कोई वस्तु किसी सरल रेखीय पथ पर गतिमान हो तो उसे सरल रेखीय गति कहते हैं |
दुरी एवं विस्थापन का उपयोग:
- दुरी एवं विस्थापन का प्रयोग वस्तु कि पूरी गति प्रक्रिया को व्यक्त करने में किया जाता है |
- दिए गए समय में वस्तु कि प्रारंभिक स्थिति के सापेक्ष अंतिम स्थिति ज्ञात करने में किया जाता है |
- जब कोई वस्तु किसी सरल रेखीय पथ पर गतिमान हो तो उसे सरल रेखीय गति कहते हैं |
दुरी एवं विस्थापन का उपयोग:
- दुरी एवं विस्थापन का प्रयोग वस्तु कि पूरी गति प्रक्रिया को व्यक्त करने में किया जाता है |
- दिए गए समय में वस्तु कि प्रारंभिक स्थिति के सापेक्ष अंतिम स्थिति ज्ञात करने में किया जाता है |
दुरी (Distance)
- यह वस्तु द्वारा तय किये गए मार्ग की कुल लम्बाई होती है |
- यह एक अदिश राशि है |
- दुरी सदैव धनात्मक होती है |
- यह विस्थापन से बड़ा या बराबर होती है |
- यह मार्ग कि लम्बाई पर निर्भर करता है |
विस्थापन (Displacement):
- यह वस्तु की प्रारंभिक स्थिति तथा अंतिम स्थिति के बीच कि न्यूनतम दुरी होती है |
- यह एक सदिश राशि हैं |
- विस्थापन धनात्मक, ऋणात्मक एवं शून्य भी हो सकता है |
- यह दुरी से छोटा अथवा बराबर होता है |
- यह मार्ग कि लंबाई पर निर्भर नहीं करता है |
एकसामान गति :
- जब कोई वस्तु समान समयांतराल में सामान दुरी तय करती है तो उसकी गति को एकसामान गति कहते हैं |
असमान गति :
- जब कोई वस्तु सामान समयांतराल में असमान दुरी तय करती है तो इस प्रकार कि गति को असमान गति कहते हैं |
चाल (speed) :
किसी वस्तु द्वारा इकाई समय में तय कि गयी दुरी को चाल कहते है |
- चाल का मात्रक मीटर (m) प्रति सेकेंड है |
- चाल के अन्य मात्रक है, सेंटीमीटर प्रति सेकंड है एवं किलोमीटर प्रति घंटा |
- चाल एक अदिश राशि है |
- यह सदा धनात्मक होता है |
- वस्तु कि गति को व्यक्त करने के लिए हमें केवल उसके परिमाण कि आवश्यकता होती है | दिशा कि कोई आवश्यकता नहीं होती है |

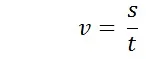
वेग (Velocity) :
जब कोई राशि किसी वस्तु की चाल में परिमाण के साथ-साथ दिशा को भी व्यक्त करे तो ऐसे चाल को वेग कहते है |
परिभाषा : एक निश्चित दिशा में वस्तु कि चाल को वेग कहते है |
वेग का मात्रक मीटर प्रति सेकंड m s-1 या m/s होता है |
- किसी वस्तु का वेग समान एवं असमान हो सकता है |
- वेग एक सदिश राशि है |
- इसमें वस्तु की चाल निश्चित दिशा में होता है |
जब एक वस्तु सीधी रेखा में बदलती हुई चाल के साथ गति कर रही है ती हम इसकी गति कि दर के परिमाण को औसत वेग के रूप में व्यक्त करते हैं |

वेग के प्रकार:
- (A) एकसमान वेग (uniform velocity): जब कोई वस्तु समान समयांतराल में समान विस्थापित होती है, तो वस्तु के इस प्रकार के वेग को एकसमान वेग कहते है |
- (B) असमान वेग (Non-uniform velocity): जब कोई वस्तु समान समयांतराल में असमान विस्थापित होती है, तो वस्तु के इस प्रकार के वेग को असमान वेग कहते है |
- (C) औसत वेग (Average velocity): किसी गतिमान वस्तु का औसत वेग उसके प्रारंभिक वेग और उसके अंतिम वेग का अंकगणितीय माध्य होता है |
चाल (speed):
- यह इकाई समय में वस्तु वस्तु द्वारा तय दुरी है |
- यह एक अदिश राशि है |
- किसी गतिमान वस्तु का औसत चाल शून्य नहीं हो सकता है |
- किसी वस्तु कि चाल हमेशा धनात्मक होता है |
वेग (velocity):
- यह इकाई समय में वस्तु द्वारा तय विस्थापन होता है |
- यह एक सदिश राशि है |
- किसी गतिमान वस्तु का औसत वेग शून्य हो सकता है |
- किसी वस्तु का वेग धनात्मक, ऋणात्मक अथवा शून्य हो सकता है |
त्वरण
त्वरण (accelaration):
इकाई समय में किसी वस्तु के वेग परिवर्तन की दर को त्वरण कहते है |
इसको ‘a’ से सूचित किया जाता है | और इसका SI मात्रक ms-2 होता है |
एकसमान सरल रेखीय गति में वेग में परिवर्तन :
- समय के साथ वेग नियत रहता है |
- इस अवस्था में किसी भी समयान्तराल में वस्तु के वेग में परिवर्तन शून्य है |
असमान गति में वेग में परिवर्तन :
- असमान गति में वेग समय के साथ परिवर्तित होता है |
- इसका मान विभिन्न समयों पर विभिन्न बिन्दुओ पर भिन्न-भिन्न होता है |
- किसी भी समयान्तराल पर वस्तु के वेग में परिवर्तन शून्य नहीं होता है |
त्वरित गति : यदि किसी वस्तु का वेग उसके आरंभिक वेग का मान u से t समय में अंतिम वेग v है और त्वरण a है तो इस प्रकार के गति को त्वरित गति कहते हैं |
सूत्र:
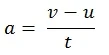
उदाहरण: यदि एक बस विराम अवस्था से शुरू होक 72 km h-1 की चाल 5 सेकंड में प्राप्त करती है जबकि वह एकसमान गति में है तो बस का त्वरण ज्ञात कीजिए |
हल:
समय (t) = 5 मिनट = 5 × 60 = 300 सेकंड
आरंभिक वेग u = 0 [∵ बस विरामावस्था में थी इसलिए आरंभिक वेग शून्य होगा ]
अंतिम वेग v = 72 km h-1
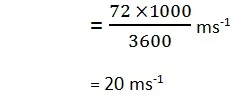
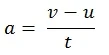
= (20 – 0)/300
= 0.066 ms-2
वस्तु का त्वरण = 0.066 ms-2
त्वरण के प्रकार :
त्वरण के प्रकार त्वरण की दिशा पर आधारित है |
ये निम्न प्रकार के हैं :
- (1) धनात्मक त्वरण :
- (2) ऋणात्मक त्वरण :
(1) धनात्मक त्वरण : जब किसी वस्तु का वेग वस्तु की गति की दिशा में समय के साथ बढ़ रहा है तो इसे धनात्मक त्वरण कहते है |
- इसमें त्वरण की दिशा वही होती है जो दिशा वस्तु की गति का होता है |
मुख्य बिन्दुएँ :
त्वरण धनात्मक होता है :
- जब त्वरण की दिशा वही होती है जो दिशा वस्तु की गति का होता है |
- जब वेग उसी दिशा में समय के साथ बढ़ता है |
- जब कोई वस्तु विरामावस्था से चलना प्रारंभ करती है |
- जब अंतिम वेग आरंभिक वेग से बड़ा हो (v > u) |
(2) ऋणात्मक त्वरण : यदि किसी वस्तु का वेग समय के साथ वस्तु की गति के विपरीत दिशा में कम हो रहा है तो इस प्रकार के त्वरण को ऋणात्मक त्वरण कहते हैं |
ऋणात्मक त्वरण को मंदन कहते हैं |
मुख्य बिन्दुएँ :
त्वरण ऋणात्मक होता है :
- जब त्वरण की दिशा वस्तु के गति के दिशा की विपरीत दिशा में हो |
- जब वेग समय के साथ कम हो रहा हो |
- जब वस्तु विरामावस्था की ओर जा रही हो |
- जब अंतिम वेग आरंभिक वेग से कम हो |
एकसमान त्वरण :
- जब किसी वस्तु का वेग समान समयांतराल में समान त्वरण उत्पन्न कर रही है तो वस्तु के ऐसे त्वरण को एकसमान त्वरण कहते हैं |
- एकसमान त्वरित गति : किसी वस्तु की गति से एकसमान त्वरण उत्पन्न हो रहा हो तो इस गति को एकसमान त्वरित गति कहते हैं |
एकसमान त्वरित गति के उदाहरण:
- चिकनी सतह पर लुढ़कते हुए गेंद की गति |
- मुक्त रूप से गिरते हुए किसी पिंड की गति |
- सूर्य के चारो ओर पृथ्वी की गति |
- एक बहुमंजिली ईमारत से नीचे आती एक तीव्र गति के लिफ्ट की गति |
- पृथ्वी के चारों ओर चन्द्रमा की गति |
असमान त्वरण :
- जब किसी वस्तु का वेग समान समयांतराल में असमान त्वरण उत्पन्न कर रही है तो वस्तु के ऐसे त्वरण को एकसमान त्वरण कहते हैं |
- असमान त्वरित गति: जब किसी वस्तु की गति से भिन्न-भिन्न त्वरण उत्पन्न हो रहा हो तो ऐसे गति को असमान त्वरित गति कहते हैं |
असमान त्वरित गति के उदाहरण:
- एक कार रेस में दौड़ती हुई कार |
- विभिन्न चाल से चलती हुई वाहन की गति |
- ऊपर की दिशा में फेंकी गई गेंद की गति |
- खुरदरे या टूटे फूटे सड़क से गुजरती हुई बस की गति |
गति का ग्राफीय प्रदर्शन :
ग्राफ का प्रयोग किसी वस्तु की गति को प्रदर्शित करने के लिए किया जाता है | अनेक प्रकार के घटनाओं के विषय में अधारभूतिक सूचनाओं को प्रदर्शित करने के लिए ग्राफ एक सुविधाजनक विधि प्रदान करता है |
उदाहरण:
- एक दिवसीय क्रिकेट मैच के प्रसारण में |
- प्रत्येक ओवर में टीम के रन रेट को दर्शाते उर्ध्वाधर दंड आलेख |
- आपने गणित के विषय में पढ़ा है कि एक सरल रेखीय ग्राफ दो चर में रैखिक समीकरणों को हल करने में मदद करता है |
भौतिकी विज्ञान में ग्राफ का प्रयोग :
- दो वस्तुओं की गति की तुलना करने लिए ग्राफ बहुत ही उपयोगी होता है |
- दुरी-समय ग्राफ से समय के किसी भी बिंदु पर वस्तु की स्थित का पता लगाया जा सकता है |
- वेग-समय ग्राफ की ढाल किसी वस्तु की त्वरण को बताता है |
- सरल रेखीय ग्राफ दो चर में रैखिक समीकरण को हल करने में मदद करता है |
- दुरी-समय ग्राफ बताता है कि कब और कहाँ कोई वस्तु किसी अन्य वस्तु को पार करती है |
- किसी वस्तु के गति का वर्णन करने के लिए एक भौतिक राशि है जैसा कि दुरी या वेग एक अन्य दूसरी राशि समय है |
गति को प्रदर्शित करने के लिए दो शर्त है :
- किसी वस्तु का समय के साथ स्थिति में परिवर्तन को दुरी-समय ग्राफ के द्वारा प्रदर्शित किया जा सकता है |
- सरल रेखा में गतिमान किसी वस्तु के लिए समय के साथ वेग में बदलाव को वेग-समय ग्राफ से प्रदर्शित किया जा सकता है |
1. दुरी-समय ग्राफ :
इस ग्राफ में :
- समय को x-अक्ष के साथ लिया जाता है और दुरी को y-अक्ष के साथ लिया जाता है |
- दुरी-समय ग्राफ को बहुत से शर्तों के अंतर्गत नियोजित किया जा सकता है जहाँ वस्तुएँ एकसमान चाल से, असमान चाल से गति करती है या विराम अवस्था में रहती है |
मुख्य अवधारणायें :
वस्तु द्वारा तय दुरी उसके द्वारा लिए गए समय के अनुक्रमानुपाती होता है |
दुरी-समय ग्राफ में दो प्रकार के ग्राफ होते हैं :
(i) एकसमान चाल के लिए दुरी-समय ग्राफ:
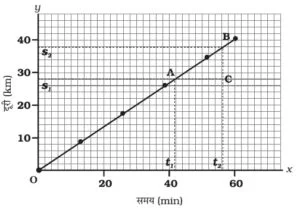
एकसमान चाल के लिए दुरी-समय ग्राफ की प्रकृति :
(a) इसका ग्राफ एक सरल रेखा होता है |
चाल के लिए सूत्र :

(ii) असमान चाल के लिए दुरी-समय ग्राफ:
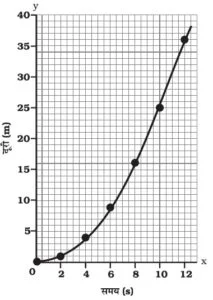
असमान चाल के लिए दुरी-समय ग्राफ की प्रकृति :
(a) इसका ग्राफ एक वक्र रेखा होता है |
वेग-समय ग्राफ :
इस ग्राफ में,
- समय को x अक्ष पर और वेग को y-अक्ष पर दर्शाया जाता है |
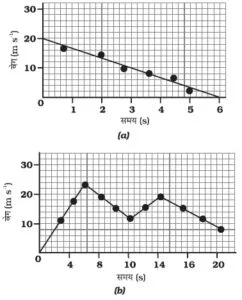
- यदि वस्तु एकसमान वेग से गतिमान है, तो समय के साथ वेग समय ग्राफ की ऊँचाई में कोई परिवर्तन नहीं होगा |
- वेग-समय ग्राफ तथा समय अक्ष के द्वारा घेरा गया क्षेत्र विस्थापन के परिणाम को बताता है |
वेग-समय ग्राफ तीन प्रकार के होते हैं |
(i) एकसमान चाल के लिए वेग-समय ग्राफ
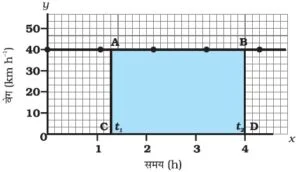
(ii) एक समान त्वरित गति के लिए वेग-समय ग्राफ
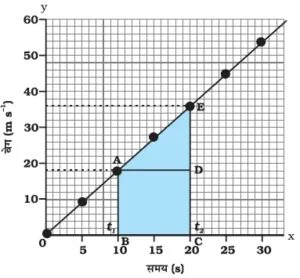
(iii) असमान त्वरित गति के लिए वेग-समय ग्राफ
ग्राफीय विधि से गति के लिए सूत्र:
ग्राफीय विधि से गति के लिए सूत्र:
कोई वस्तु सीधी रेखा में एकसमान त्वरण से चलती है तो एक निश्चित समयांतराल में समीकरणों के द्वारा उसके वेग, गति के दौरान त्वरण व उसके द्वारा तय की गई दूरी में जो संबंध स्थापित होता है, उस समीकरण को गति का समीकरण कहा जाता है | ये समीकरण तीन हैं –
(i) v = u + at
(ii) s = ut + ½ at2
(iii) 2 as = v2 – u2
गति के समीकरण को प्राप्त करने के लिए वेग-समय ग्राफ –
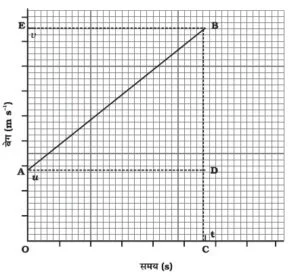
- इस वेग समय ग्राफ में OE रेखा या BC रेखा वेग को प्रदर्शित करता है जबकि OC रेखा समय को प्रदर्शित करता है |
- BE तिरछी रेखा समयानुसार वेग में परिवर्तन (त्वरण) को प्रदर्शित करता है |
- वेग समय ग्राफ से वस्तु के त्वरण को व्यक्त किया जाता है |
(i) v = u + at के लिए हल :
अब, BC = BD + DC
= BD + OA …………. (i)
यहाँ आरंभिक वेग (u) = OA है और
अंतिम वेग (v) = BC है |
इसलिए, BC = v तथा OA = u रखने पर
BC = BD + OA समी० (i) से
या v = BD + u
या BD = v – u
अत: वेग में परिवर्तन BD = v – u ………… (ii)
लिया गया कुल समय (t) = OC

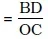
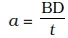
BD = at ………… (iii)
समीकरण (ii) तथा (iii) से
v – u = at
या v = u + at
या v = u + at
(ii) s = ut + ½ at2 के लिए हल :
अब,
माना वस्तु ने एकसमान त्वरण a से t समय लगाकर s दुरी तय की |
वस्तु द्वारा तय की गई दुरी = वेग-समय ग्राफ में AB के नीचे घिरे क्षेत्र OABC का क्षेत्रफल
अत : s = समलंब OABC का क्षेत्रफल
या = आयात OADC का क्षेत्रफल + त्रिभुज ABD का क्षेत्रफल
= OA × OC + ½ (AD × BD)
= u × t + ½ × (t × at) [चूँकि BD = at] समी० (iii) से
= ut + ½ at2
अत: s = ut + ½ at2
(iii) 2 as = v2 – u2 के लिए हल :
अब, उसी प्रकार
वेग समय ग्राफ से –
v – u = at
या
s = समलंब OABC का क्षेत्रफल
= ½ (समांतर भुजाओं का योग’) × ऊँचाई
= ½ (OA + BC) × OC
= ½ (u + v) × t समी० (1) से
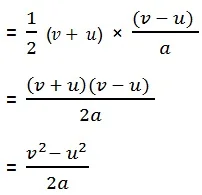
या 2 a s = v2 – u2
Comments are closed