Whole Numbers Class 6 Extra Questions Maths Chapter 2
Whole Numbers Class 6 Extra Questions Very Short Answer Type
Question 1.
Write the smallest whole number.
Solution:
0 is the smallest whole number.
Question 2.
What is the predecessor of whole number 0?
Solution:
Whole number 0 has no predecessor.
Question 3.
Which property do the following statements hold?
(a) 6 + 4 = 4 + 6
(b) 3 + 2 = whole number
Solution:
(a) 6 + 4 = 4 + 6 holds commutative property of addition
(b) 3 + 2 = whole number holds closure property.
Question 4.
Add the following in three ways. Indicate the property used.
(a) 25 + 36 + 15
(b) 30 + 18 + 22
Solution:
(a) 25 + 36 + 15
Way I: 25 + (36 + 15) = 25 + 51 = 76
Way II: (25 + 36) + 15 = 61 + 15 = 76
Way III: (25 + 15) + 36 = 40 + 36 = 76
Here, we have used associative property.
(b) 30 + 18 + 22
Way I: 30 + (18 + 22) = 30 + 40 = 70
Way II: (30 + 18) + 22 = 48 + 22 = 70
Way III: (30 + 22) + 18 = 52 + 18 = 70
Here, we have used associative property.
Question 5.
Using distributive property, solve the following:
(а) 360 x 102
(b) 35 x 98
Solution:
(a) 36 x 102 = 36 x (100 + 2)
= 36 x 100 + 36 x 2
= -36000 + 72 = 36072
(b) 35 x 98 = 35 x (100 – 2) = 35 x 100 – 35 x 2
= 3500 – 70 = 3430
Question 6.
Find the product of the greatest 3-digit number and the smallest 2-digit number.
Solution:
The greatest 3-digit number = 999
The smallest 2-digit number = 10
∴ Product = 999 x 10 = 9990
Question 7.
Write any two numbers which can be shown as rectangles.
Solution:
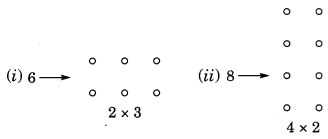
Question 8.
Write the predecessor of the smallest 4-digit number.
Solution:
The smallest 4-digit number = 1000
∴ The predecessor of 1000 = 1000 – 1 = 999
Question 9.
For n = 5, verify the given statement 10 x n + 1 = n1
Solution:
Given statement is
10 x n + 1 = n1
Put n = 5, 10 x 5 + 1 = 51
⇒ 50 + 1 = 51
⇒ 51 = 51. Hence, verified.
Question 10.
Write the next two steps:
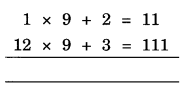
Solution:
Next two steps are 123 x 9 + 4 = 1111 and 1234 x 9 + 5 = 11111.
Whole Numbers Class 6 Extra Questions Short Answer Type
Question 11.
Using the properties, find the values of each of the following:
(a) 736 x 102
(b) 8165 x 169 – 8165 x 69
Solution:
(a) 736 x 102 = 736 x (100 + 2)
= 736 x 100 + 736 x 2 [Using distributive property]
= 73600 + 1472 = 75072
(b) 8165 x 169 – 8165 x 69 = 8165 x (169 – 69) [Using distributive property]
= 8165 x 100 = 816500
Question 12.
Observe the following patterns and extend them by two more terms.

Solution:
Next two terms are
1010101 × 1010101= 1020304030201
101010101 × 101010101=10203040504030201
Question 13.
Observe the following patterns and extend them by two more terms:
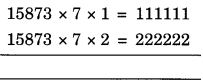
Solution:
Next two terms are
15873 x 7 x 3 = 333333
15873 x 7 x 4 = 444444
Question 14.
Write the three whole numbers which can be arranged as squares.
Solution:
The required number are 4, 9, 16.
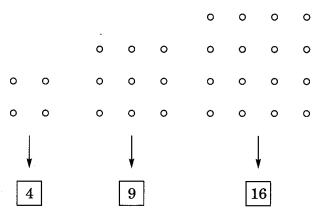
Question 15.
Using the properties of whole numbers, find the value of the following in suitable way:
(a) 945 x 4 x 25
(b) 40 x 328 x 25
Solution:
(a) 945 x 4 x 25 = 945 x (4 x 25)
= 945 x 100 = 94500
(b) 40 x 328 x 25 = 328 x (40 x 25)
= 328 x 1000 = 328000
Question 16.
Represent the following on number line:
(a) 3 + 4
(b) 6 – 2
(c) 2 × 4
Solution:
(a) 3 + 4

(b) 6 – 2
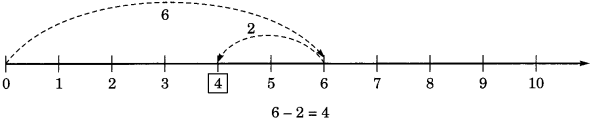
(c) 2 × 4

Question 17.
Give one example for each of the following properties for whole numbers.
(a) Closure property
(b) Commutative property
(c) Associative property
(d) Distributive property
Solution:
(a) 3 + 4 = 7 (whole number) closure property
(b) 4 + 5 = 5 + 4 Commutative property
(c) 3 + (5 + 7) = (3 + 5) + 7 Associative property
(d) 6 x (8 + 3) = 6 x 8 + 6 x 3 Distributive property.
Question 18.
A dealer purchased 124 LED sets. If the cost of one set is ₹38,540, determine their total cost.
Solution:
Total cost of 124 LED sets = ₹(38,540 x 124)
= ₹ [38,540 x (100 + 20 + 4)]
= ₹ [38,540 x 100 + 38,540 x 20 + 38,540 x 4]
= ₹ [38,54,000 + 7,70,800 + 1,54,160]
= ₹ 47,789,60
Question 19.
Find the product of the greatest 3-digit number and the greatest 2-digit number.
Solution:
Greatest 3-digit number = 999
Greatest 2-digit number = 99
∴ Product = 999 x 99 = 999 x (100 – 1)
= 999 x 100 – 999 x 1
= 99900 – 999 = 98901
Question 20.
Write 10 such numbers which can be shown only as line.
Solution:
2, 5, 7, 11, 13, 17, 19, 23, 29 and 31 are such numbers which can be shown only as line.
123 x 9 + 4 = 1111.
Whole Numbers Class 6 Extra Questions Long Answer Type
Question 21.
320 km distance is to be covered partially by bus and partially by train. Bus covers 180 km distance with a speed of 40 km/h and the rest of the distance is covered by the train at a speed of 70 km/h. Find the time taken by a passenger to cover the whole distance.
Solution:
Total distance = 320 km
Distance covered by the bus = 180 km
Speed of the bus = 40 km/h
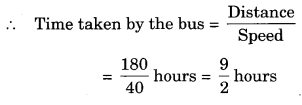
Distance covered by the train = 320 – 180 = 140 km.
Speed of the train = 70 km/h
∴ Time taken by the train
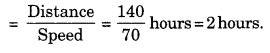
Hence, the total time taken by the passenger
= (frac { 9 }{ 2 }) hours + 2 hours
= 4 hours 30 min + 2 hours
= 6 hours 30 min
Question 22.
Solve the following and establish a pattern:
(a) 84 x 9
(b) 84 x 99
(c) 84 x 999
(d) 84 x 9999
Solution:
(a) 84 x 9 = 84 x (10 – 1) = 84 x 10 – 84 x 1 = 840 – 84 = 756
(b) 84 x 99 = 84 x (100 – 1) = 84 x 100 – 84 x 1 = 8400 – 84 = 8316
(c) 84 x 999 = 84 x (1000 – 1) = 84 x 1000 – 84 x 1 = 84000 – 84 = 83916
(d) 84 x 9999 = 84 x (10000 – 1) = 84 x 10000 – 84 x 1 = 840000 – 84 = 839916
Question 23.
Solve the following with suitable and short-cut method: .
(a) 86 x 5
(b) 86 x 15
(c) 86 x 25
(d) 86 x 35
(e) 86 x 50
(f) 96 x 125
(g) 96 x 250
(h) 112 x 625
Solution:

Question 24.
Ramesh buys 10 containers of juice from one shop and 18 containers of the same juice from another shop. If the capacity of each container is same and the cost of each of the container is ₹150, find the total money spend by Ramesh.
Solution:
Ramesh buys 10 containers from one shop Cost of 1 container = ₹150
He buys 18 containers of the same capacity from another shop.
Cost of 1 container = ₹150
∴ Total money spent by Ramesh
= ₹ [10 x 150 + 18 x 150]
= ₹150 x (10 + 18)
= ₹150 x 28
= ₹4200
Question 25.
Fill in the blanks.
(а) The smallest whole number is ……… .
(b) The smallest natural number is ……… .
(c) Difference between 5-digit smallest number and 4-digit largest number is ……… .
(d) Any number divided by 0 is not ……… .
(e) The property used in 84 x 25 = 25 x 84 is ……… .
(f) The property used in 80 x (60 + 3) = 80 x 60 + 80 x 3 is ……… .
(g) The smallest number which can be shown by two doted rectangles is ……… .
(h) Every whole number except ……… is a natural number.
(i) When any counting number is multiplied by zero, the product is ……… .
(j) When zero is divided by any non-zero whole number, the quotient is ……… .
Solution:
(a) The smallest whole number is 0.
(b) The smallest natural number is 1.
(c) Difference between 5-digit smallest number and 4-digit largest number is 1.
(d) Any number divided by 0 is not defined.
(e) The property used in 84 x 25 = 25 x 84 is commutative property.
(f) The property used in 80 x (60 + 3) = 80 x 60 + 80 x 3 is distributive property.
(g) The smallest number which can be shown by two doted rectangles is 6.
(h) Every whole number except 0 is a natural number.
(i) When any counting number is multiplied by zero, the product is 0.
(j) When zero is divided by any non-zero whole number, the product is 0.
Question 26.
Which of the following statements are true (T) and which are false (F)?
(a) The sum of two whole numbers is always less than their product.
(b) There is only one whole number n such that n x n – n
(c) For two non-zero whole numbers a and b, a ÷ b = b ÷ a.
(d) The sum of two odd whole numbers is an even number.
(e) There jloes not exist any whole number m for which m ÷ m = m.
(f) (16 ÷ 4) ÷ 2 = 16 ÷ (4 ÷ 2)
(g) 7 – 8 = whole number
(h) If 1 is added to a number, we get its successor.
(i) The whole number 15 lies between 14 and 21.
(j) 84 x (10 + 5) = 84 x 10 + 84 x 5 represents distributive property.
Solution:
(a) False statement
(b) False statement
(c) False statement
(d) True statement
(e) False statement
(f) False statement
(g) False statement
(h) True statement
(i) True statement
(j) True statement.
Question 27.
The value of 27 ÷ (9 ÷ 3) is
(a) 3
(b) 6
(c) 9
(d) 27
Solution:
27 ÷ (9 ÷ 3) = 27 ÷ ((frac { 9 }{ 3 })) = 27 ÷ 3 = 9
Hence, the correct option is (c).
Question 28.
The whole number 7 can be arranged as,
(a) line
(b) square
(c) rectangle
(d) triangle
Solution:
7 can be arranged as line.
Hence, the correct option is (a).
Whole Numbers Class 6 Extra Questions Higher Order Thinking Skills (HOTS)
Question 29.
A housing complex built by DLF consists of 25 large buildings and 40 small buildings. Each large building has 15 floors with 4 apartments on each floor and each small building has 9 floors with 3 apartments on each floor. How many apartments are there in all?
Solution:
Number of large buildings = 25
Number of floors = 15
Number of apartments on each floor = 4
∴ Total number of apartments in large buildings = 25 x 15 x 4
Number of small building = 40
Number of floors = 9
Number of apartments on each floor = 3
∴ Total number of apartments in small buildings = 40 x 9 x 3
Hence, the number of apartments in all = 25 x 15 x 4 + 40 x 9 x 3 = 1500 + 1080 = 2580.
Question 30.
A school principal places orders for 85 chairs and 25 tables with a dealer. Each chair cost ₹180 and each table cost ₹140. If the principal has given ₹2500 to the dealer as an advance money, then what amount to be given to the dealer now?
Solution:
Number of chairs = 85
Cost of one chair = ₹ 180
Cost of 85 chairs = ₹ (85 x 180)
Number of tables = 25
Cost of one table = ₹ 140
Cost of 25 tables = ₹ (25 x 140)
Total cost of all chairs and tables = ₹(85 x 180 + 25 x 140)
= ₹ (15300 + 3500) = ₹ 18800
Money given in advance = ₹ 2500
∴ Balance money to be paid to the dealer = ₹ 18800 – ₹ 2500 = ₹ 16300
<!– –>
Comments are closed