NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.2
NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Exercise 12.2
Ex 12.2 Class 7 Maths Question 1.
Simplify combining like terms:
(i) 21b -32 + 7b- 206
(ii) -z2 + 13z2 -5z + 7z3 – 152
(iii) p – (p – q) – q – (q – p)
(iv) 3a – 2b — ab – (a – b + ab) + 3ab + 6 – a
(v) 5x2y – 5×2 + 3yx2 – 3y2 + x2 – y2 + 8xy2 -3y2
(vi) (3y2 + 5y – 4) – (8y – y2 – 4)
Solution:
(i) 21b – 32 + 7b – 206
Re-arranging the like terms, we get
216 + 7b – 206 – 32
= (21 + 7 – 20)b – 32
= 8b – 32 which is required.
(ii) -z2 + 13z2 – 5z – 15z
Re-arranging the like terms, we get
7z3 – z2 + 13z2 – 5z + 5z – 15z
= 7z3 + (-1 + 13)z2 + (-5 – 15)z
= 7z3 + 12z2 – 20z which is required.
(iii) p – (p – q) – q – (q – p)
=p – p + q – q – q + p
Re-arranging the like terms, we get

= p – q which is required.
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
= 3a – 2b – ab – a + b – ab + 3ab + b – a
Re-arranging the like terms, we get
= 3a – a – a – 2b + b + b – ab – ab + 3ab

= a + ab which is required.
(v) 5x2y – 5×2 + 3yx2 – 3y2 + x2 – y2 + 8xy2 – 3y2
Re-arranging the like terms, we get
5x2y + 3x2y + 8xy2 – 5×2 + x2 – 3y2 – y2 – 3y2
= 8x2y + 8xy2 – 4×2 – 7y2 which is required.
(vi) (3y2 + 5y – 4) – (8y – y2 – 4)
= 3y2 + 5y – 4 – 8y + y2 + 4 (Solving the brackets)
Re-arranging the like terms, we get
= 3y2 + y2 + 5y – 8y – 4 + 4
= 4y2 – 3y which is required.
Ex 12.2 Class 7 Maths Question 2.
Add:
(i) 3mn, -5mn, 8mn, -4mn
(ii) t – 8tz, 3tz, -z, z – t
(iii) -7mn + 5, 12mn + 2, 9mn – 8, -2mn – 3
(iv) a + b – 3, b – a + 3, a – b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
(vii) 4x2y, -3xy2, -5xy2, 5x2y
(viii) 3p2q2 – 4pq + 5, -10p2q2, 15 + 9pq + 7p2q2
(ix) ab – 4a, 4b – ab, 4a – 4b
(x) x2 – y2 – 1, y2 – 1 – x2, 1 – x2 – y2
Solution:
(i) 3mn, -5mn, 8mn, -4mn
= (3 mn) + (-5 mn) + (8 mn) + (- 4 mn)
= (3 – 5 + 8 – 4)mn
= 2mn which is required.
(ii) t – 8tz, 3tz – z, z – t
t – 8tz + 3tz – z + z – t
Re-arranging the like terms, we get
t – t – 8tz + 3tz – z + z
⇒ 0 – 5 tz + 0
⇒ -5tz which is required.
(iii) -7mn + 5, 12mn + 2, 9mn – 8, -2mn – 3
= -7mn + 5 + 12mn + 2 + 9mn – 8 + (-2mn) – 3
Re-arranging the like terms, we get
-7mn + 12 mn + 9mn – 2 mn + 5 + 2 – 8 – 3

= 12 mn – 4 which is required.
(iv) a + b – 3, b – a + 3, a – b + 3
⇒ a + b – 3 + b – a + 3 + a – b + 3
Re-arranging the like terms, we get
a – a + a + b + b – b – 3 + 3 + 3
⇒ a + b + 3 which is required.
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
∴ 14x + 14y – 12xy – 13 + 18 – 7x – 10y + 8xy + 4xy
Re-arranging the like terms, we get
-12xy + 8xy + 4xy + 14x – 7x + 10y – 10y – 13 + 18

= 0 + 7x + 0 + 5
= 7x + 5 which is required
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5 5m -In + 3n — 4m + 2 + 2m – 3mn – 5
Re-arranging the like terms, we get
5m – 4m + 2m – 7n + 3n- 3mn + 2 – 5
= 3m – 4n – 3mn – 3 which is required.
(vii) 4x2y, -3xy2, -5xy2, 5x2y
Re-arranging the like terms and adding, we get
4x2y – 5xy2 – 3xy2 + 5x2y
=9x2y — 8xy2 which is required.
(viii) 3p2q2 – 4pq + 5, -10p2q2, 15 + 9pq + 7p2q2
= (3p2q2 – 4pq + 5) + (-10p2q2) + (15 + 9pq + 7p2q2)
= 3p2q2 – 4pq + 5 – 10p2q2 + (15 + 9pq + 7p2q2 )
= 3p2q2 + 7p2q2 – 10p2q2 – 4pq + 9pq + 5 + 15
= 10p2q2 – 10p2q2 + 5pq + 20
= 0 + 5pq + 20
= 5pq + 20 which is required.
(ix) ab – 4a, 4b – ab, 4a – 4b
= ab – 4a + 4b – ab + 4a – 4b

= 0 + 0 + 0 = 0 which is required.
(x) x2 – y2 – 1, y2 – 1 – x2, 1 – x2 – y2
= x2 – y2 – 1 + y2 – 1 – x2 + 1 – x2 – y2
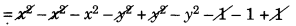
= -x2 – y2 – 1
= -(x2 + y2 + 1) which is required.
Ex 12.2 Class 7 Maths Question 3.
Subtract:
(i) -5y2 from y2
(ii) 6xy from -12xy
(iii) (a – b) from (a + b)
(iv) a(b – 5) from b(5 – a)
(v) -m2 + 5mn from 4m2 – 3mn + 8
(vi) -x2 + 10x – 5 from 5x – 10
(vii) 5a2 – 7ab + 5b2 from 3ab – 2a2 – 2b2
(viii) 4pq – 5q2 – 3p2 from 5p2 + 3q2 – pq
Solution:
(i) -5y2 from y2 = y2 – (-5y2)
= y2 + 5y2 = 6y2
(ii) 6ry from -12ry = -12xy – 6xy = -18xy which is required.
(iii) (a – b) from (a + b)
= (a + b) – (a – b)
= a + b – a + b = 2b which is required
(iv) a(b – 5) from b(5 – a)
= b(5 – a) – a(b – 5)
= 5b – ab – ab + 5a
= 5a – 2ab + 5b
= 5a + 5b – 2ab which is required.
(v) -m2 + 5mn from 4m2 – 3mn + 8
= (4m2 – 3mn + 8) – (-m2 + 5mn)
= 4m2 – 3mn + 8 + m2 – 5mn
= 4m2 + m2 – 3mn – 5mn + 8
= 5m2 – 8mn + 8 which is required.
(vi) -x2 + 10x – 5 from 5x – 10
= (5x – 10) – (-x2 + 10x – 5)
= 5x – 10 + x2 – 10x + 5
= x2 + 5x – 10x – 10 + 5
= x2 – 5x – 5 which is required.
(vii) 5a2 – 7ab + 5b2 from 3ab – 2a2 – 2b2
= (3ab – 2a2 – 2b2) – (5a2 – 7ab + 5b2)
= 3ab – 2a2 – 2b2 – 5a2 + 7ab – 5b2
= 3ab + 7ab – 2a2 – 5a2 – 2b2 – 5b2
= 10ab – 7a2 – 7b2
which is required.
(viii) 4pq – 5q2 – 3p2 from 5p2 + 3q2 – pq
= (5p2 + 3q2 – pq) – (4pq – 5q2 – 3p2)
= 5p2 + 3q2 – pq – 4pq + 5q2 + 3p2
= 5p2 + 3p2 + 3q2 + 5q2 – pq – 4pq
= 8p2 + 8q2 – 5pq
which is required.
Ex 12.2 Class 7 Maths Question 4.
(a) What should be added to x2 + xy + y2to obtain 2×2 + 3xy?
(b) What should be subtracted from 2a + 8b + 10 to get -3a + 7b + 16?
Solution:
(a) (2×2 + 3xy) – (x2 + xy + y2)
= 2×2 + 3xy – x2 – xy – y2
= 2×2 – x2 + 3xy – xy – y2
= x2 + 2xy – y2 is required expression.
(b) (2a + 8b + 10) – (-3a + 7b + 16)
= 2a + 8b + 10 + 3a – 7b – 16
= 2a + 3a + 8b – 7b + 10 – 16
= 5a + b – 6 is required expression.
Ex 12.2 Class 7 Maths Question 5.
What should be taken away from 3×2 – 4y2 + 5xy + 20 to obtain -x2 – y2 + 6xy + 20?
Solution:
Let A be taken away.
∴ (3×2 – 4y2 + 5 xy + 20)-A
= -x2 – y2 + 6xy + 20
⇒ A = (3×2 – 4y2 + 5xy + 20) – (-x22 – y2 + 6xy + 20)
= 3×2 – 4y2 + 5xy + 20 + x2 + y2 – 6xy – 20
= 3×2 + x2 – 4y2 + y2 + 5xy – 6xy + 20 – 20
= 4×2 – 3y2 – xy is required expression.
Ex 12.2 Class 7 Maths Question 6.
(a) From the sum of 3x – y + 11 and -y – 11, subtract 3x – y – 11.
(b) From the sum of 4 + 3x and 5 – 4x + 2×2, subtract the sum of 3×2 – 5x and -x2 + 2x + 5.
Solution:
(a) Sum of 3x – y + 11 and -y – 11
= (3x – y + 11) + (-y – 11)
= 3x – y + 11 – y – 11
∴ 3x – 2y – (3x – 2y) – (3x – y – 11)
= 3x – 2y – 3x + y + 11
= 3x – 3x – 2y + y + 11
= -y + 11 is required solution.
(b) Sum of (4 + 3x) and (5 – 4x + 2×2)
= 4 + 3x + 5 – 4x + 2×2
= 2×2 – 4x + 3x + 9 = 2×2 – x + 9
Sum of (3×2 – 5x) and (-x2 + 2x + 5)
= (3×2 – 5x) + (-x2 + 2x + 5)
= 3×2 – 5x – x2 + 2x + 5 = 2×2 – 3x + 5
Now (2×2 – x + 9) – (2×2 – 3x + 5)
= 2×2 – x + 9 – 2×2 + 3x – 5
= 2×2 – 2×2 + 3x – x + 4
= 2x + 4 is required expression.






<!– –>
Comments are closed