NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.3
NCERT Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Exercise 12.3
Ex 12.3 Class 7 Maths Question 1.
If m = 2, find the value of:
(i) m – 2
(ii) 3m – 5
(iii) 9 – 5m
(iv) 3m2 – 2m – 7
(v) (frac{5 m}{2}-4)
Solution:
(i) m – 2
Putting m = 2, we get
2 – 2 = 0
(ii) 3m – 5
Putting m = 2, we get
3 × 2 – 5 = 6 – 5 = 1
(iii) 9 – 5m
Putting m = 2, we get
9 – 5 × 2 = 9 – 10 = -1
(iv) 3m2 – 2m – 7 Putting m = 2, we get
3(2)2 – 2(2) – 7 = 3 × 4 – 4 – 7
=12 – 4 – 7 = 12 – 11 = 1
(v) (frac{5 m}{2}-4)
Putting m = 2, we get
(frac{5 times 2}{2}-4=5-4=1)
Ex 12.3 Class 7 Maths Question 2.
If p = -2, find the value of:
(i) 4p + 7
(ii) -3p2 + 4p + 7
(iii) -2p3 – 3p2 + 4p + 7
Solution:
(i) 4p + 7
Putting p = -2, we get 4(-2) + 7 = -8 + 7 = -1
(ii) -3p2 + 4p + l
Putting p = -2, we get
-3(-2)2 + 4(-2) + 7
= -3 × 4 – 8 + 7 = -12 – 8+ 7 = -13
(iii) -2p3 – 3p2 + 4p + 7
Putting p = -2, we get
– 2(-2)3 – 3(-2)2 + 4(-2) + 7
= -2 × (-8) – 3 × 4 – 8 + 7
= 16 – 12 – 8 + 7 = 3
Ex 12.3 Class 7 Maths Question 3.
If a = 2, b = -2, find the value of:
(i) a2 + b2
(ii) a2 + ab + b2
(iii) a2 – b2
Solution:
(i) a2 + b2
Putting a = 2 and b = -2, we get
(2)2 + (-2)2 = 4 + 4 = 8
(ii) a2 + ab + b2
Putting a = 2 and b = -2, we get
(2)2 + 2(-2) + (-2)2 = 4 – 4 + 4 = 4
(iii) a2 – b2
Putting a = 2 and b = -2, we get
(2)2 – (-2)2 = 4 – 4 = 0
Ex 12.3 Class 7 Maths Question 4.
When a = 0, b = -1, find the value of the given expressions:
(i) 2a + 2b
(ii) 2a2 + b2 + 1
(iii) 2a2b + 2ab2 + ab
(iv) a2 + ab + 2
Solution:
(i) 2a + 2b = 2(0) + 2(-1)
= 0 – 2 = -2 which is required.
(ii) 2a2 + b2 + 1
= 2(0)2 + (-1)2 + 1 =0 + 1 + 1 = 2 which is required.
(iii) 2a2b + 2ab2 + ab
= 2(0)2 (-1) + 2(0)(-1)2 + (0)(-1)
=0 + 0 + 0 = 0 which is required.
(iv) a2 + ab + 2
= (0)2 + (0)(-1) + 2
= 0 + 0 + 2 = 0 which is required.
Ex 12.3 Class 7 Maths Question 5.
Simplify the expressions and find the value if x is equal to 2.
(i) x + 7 +4(x – 5)
(ii) 3(x + 2) + 5x – 7
(iii) 6x + 5(x – 2)
(iv) 4(2x – 1) + 3x + 11
Solution:
(i) x + 7 + 4(x – 5) = x + 7 + 4x – 20 = 5x – 13
Putting x = 2, we get
= 5 × 2 – 13 = 10 – 13 = -3
which is required.
(ii) 3(x + 2) + 5x – 7 = 3x + 6 + 5x -7 = 8x – 1
Putting x = 2, we get
= 8 × 2 – 1 = 16 – 1 = 15
which is required.
(iii) 6x + 5(x – 2) = 6x + 5x – 10
= 11 × – 10
Putting x = 2, we get
= 11 × 2 – 10 = 22 – 10 = 12
which is required.
(iv) 4(2x – 1) + 3x + 11 = 8x – 4 + 3x + 11
= 11x + 7
Putting x = 2, we get
= 11 × 2 + 7 = 22+ 7 = 29
Ex 12.3 Class 7 Maths Question 6.
Simplify these expressions and find their values if x = 3, a = -1, b = -2.
(i) 3x – 5 – x + 9
(ii) 2 – 8x + 4x + 4
(iii) 3a + 5 – 8a + 1
(iv) 10 – 3b – 4 – 55
(v) 2a – 2b – 4 – 5 + a
Solution:
(i) 3x – 5 – x + 9 = 2x + 4
Putting x = 3, we get
2 × 3 + 4 = 6 + 4 = 10
which is required.
(ii) 2 – 8x + 4x + 4 = -8x + 4x + 2 + 4 = -4x + 6
Putting x = 2, we have
= -4 × 2 + 6 = -8 + 6 =-2
which is required.
(iii) 3a + 5 – 8a +1 = 3a – 8a + 5 + 1 = -5a + 6
Putting a = -1, we get
= -5(-1) + 6 = 5 + 6 = 11
which is required.
(iv) 10 – 3b – 4 – 5b = -3b – 5b + 10 – 4
= -8b + 6
Putting b = -2, we get
= -8(-2) + 6 = 16 + 6 = 22
which is required.
(v) 2a – 2b – 4 – 5 + a = 2a + a – 2b – 4 – 5
= 3a – 26 – 9
Putting a = -1 and b = -2, we get
= 3(-1) – 2(-2) – 9
= -3 + 4 – 9 = 1 – 9 = -8
which is required.
Ex 12.3 Class 7 Maths Question 7.
(i) If z = 10, find the value of z2 – 3(z – 10).
(ii) If p = -10, find the value of p2 -2p – 100.
Solution:
(i) z2 – 3(z – 10)
= z2 – 3z + 30
Putting z = 10, we get
= (10)2 – 3(10) + 30
= 1000 – 30 + 30 = 1000 which is required.
(ii) p2 – 2p – 100
Putting p = -10, we get
(-10)2 – 2(-10) – 100
= 100 + 20 – 100 = 20 which is required.
Ex 12.3 Class 7 Maths Question 8.
What should be the value of a if the value of 2×2 + x – a equals to 5, when x = 0?
Solution:
2×2 + x – a = 5
Putting x = 0, we get
2(0)2 + (0) – a = 5
0 + 0 – a = 5
-a = 5
⇒ a = -5 which is required value.
Ex 12.3 Class 7 Maths Question 9.
Simplify the expression and find its value when a = 5 and b = -3.
2(a2 + ab) + 3 – ab
Solution:
2(a2 + ab) + 3 – ab = 2a2 + 2ab + 3 – ab
= 2a2 + 2ab – ab + 3
= 2ab + ab + 3
Putting, a = 5 and b = -3, we get
= 2(5)2 + (5)(-3) + 3
= 2 × 25 – 15 + 3
= 50 – 15 + 3
= 53 – 15 = 38
Hence, the required value = 38.
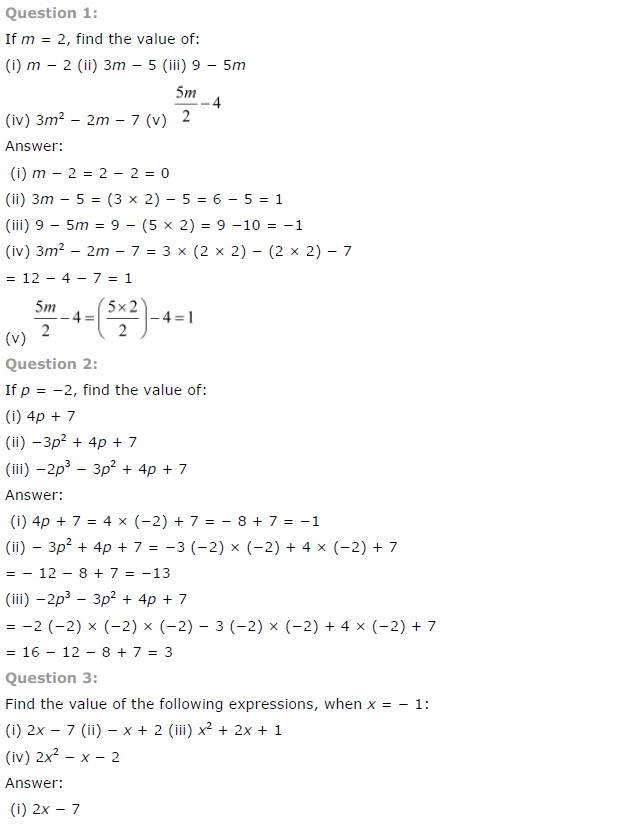



<!– –>
Comments are closed