NCERT Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.1
NCERT Solutions for Class 7 Maths Chapter 13 Exponents and Powers Exercise 13.1
Ex 13.1 Class 7 Maths Question 1.
Find the value of
(i) 26
(ii) 93
(iii) 112
(iv) 54
Solution:
(i) 26 = 2 × 2 × 2 × 2 × 2 × 2 = 64
(ii) 93 = 9 × 9 × 9 = 729
(iii) 112 = 11 × 11 = 121
(iv) 54 = 5 × 5 × 5 × 5 = 625
Ex 13.1 Class 7 Maths Question 2.
Exress the following in exponential form:
(i) 6 × 6 × 6 × 6
(ii) t × t
(iii) b × b × b × b
(iv) 5 × 5 × 7 × 7 × 7
(v) 2 × 2 × a × a
(vi) a × a × a × c × c × c× c × d
Solution:
(i) 6 × 6 × 6 × 6 = 63
(ii) t × t = t2
(iii) b × b × b × b = b4
(iv) 5 × 5× 7 × 7 × 7 = 52 × 73 = 52 · 73
(v) 2 × 2 × a × a = 22 × a2 = 22 · a2
(vi) a × a ×a × c × c × c × c × d = a3 × c4 × d = a3 · c4 · d
Ex 13.1 Class 7 Maths Question 3.
Express each of the following numbers using exponential notation:
(i) 512
(ii) 343
(iii) 729
(iv) 3125
Solution:
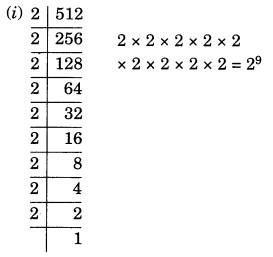

Ex 13.1 Class 7 Maths Question 4.
Identify the greater number, wherever possible, in each of the following?
(i) 43 or 34
(ii) 53 or 35
(iii) 28 or 82
(iv) 1002 or 2100
(v) 210 or 102
Solution:
(i) 43 or 34
43 = 4 × 4 × 4 = 64,
34 = 3 × 3 × 3 × 3 = 81
Since 81 > 64
∴ 34 is greater than 43.
(ii) 53 or 35
53 = 5 × 5 × 5 = 125
35 = 3 × 3 × 3 × 3 × 3 = 243
Since 243 > 125
∴ 35 is greater than 53.
(iii) 28 or 82
28 =2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
82 = 8 × 8 = 64
Since 256 > 64
∴ 28 is greater than 28.
(iv) 1002 or 2100
1002 = 100 × 100 = 10000
2100 = 2 × 2 × 2 × … 100 times
Here 2 × 2 × 2 ×2 × 2 × 2 × 2 ×2 × 2 × 2 × 2 × 2 × 2 × 2 = 214 = 16384
Since 16384 > 10,000
∴ 2100 is greater than 1002.
(v) 210 or 102
210 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
102 = 10 × 10 = 100
Since 1024 > 100
∴ 210 is greater than 102.
Ex 13.1 Class 7 Maths Question 5.
Express each of the following as the product of powers of their prime
(i) 648
(ii) 405
(iii) 540
(iv) 3600
Solution:

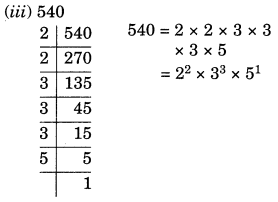

Ex 13.1 Class 7 Maths Question 6.
Simplify:
(i) 2 × 103
(ii) 72 × 22
(iii) 23 × 5
(iv) 3 × 44
(v) 0 × 102
(vi) 52 × 33
(vii) 24 × 32
(viii) 32 × 104
Solution:
(i) 2 × 103 = 2 × 10 × 10 × 10 = = 2000
(ii) 72 × 22 = = 7 × 7 × 2 × 2 = 196
(iii) 23 × 5 = 2 × 2 × 2 × 5 = 40
(iv) 3 × 44 = 3 × 4 × 4 × 4 × 4 = 768
(v) 0 × 102 = 0 × 10 × 10 = = 0
(vi) 52 × 33 = 5 × 5 × 3 × 3 × 3 = 675
(vii) 24 × 32 = 2 × 2 × 2 × 2 × 3 × 3 = 144
(viii) 32 × 104 = 3 × 3 × 10 × 10 × 10 × 10 = 90000
Ex 13.1 Class 7 Maths Question 7.
Simplify:
(i) (-4)3
(ii) (-3) × (-2)3
(iii) (-3)2 × (-5)2
(iv) (-2)3 × (-10)3
Solution:
(i) (-4)2 = (-4) × (-4) × (-4) = -64 [∵ (-a)odd number = -aodd number]
(ii) (-3) × (-2)3 = (-3) × (-2) × (-2) × (-2)
= (-3) × (-8) = 24
(iii) (-3)2 × (-5)2 = [(-3) × (-5)]2
= 152 = 225 [∵ am × bm = (ab)m)
(iv) (-2)3 × (-10)3 = [(-2) × (-10)]3
= 202 = 8000 [∵ am × bm = (ab)m]
Ex 13.1 Class 7 Maths Question 8.
Compare the following:
(i) 2.7 × 1012; 1.5 × 108
(ii) 4 × 1014; 3 × 1014
Solution:
(i) 2.7 × 1012; 1.5 × 108
Here, 1012 > 108
∴ 2.7 × 1012> 1.5 × 108
(ii) 4 × 1014; 3 × 1017
Here, 1017 > 1014
∴ 4 × 1014 < 3 × 1017




<!– –>
Comments are closed