Surface Areas and Volumes Class 9 Maths Formulas

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.9

Ex 13.9 Class 9 Maths Question 1.
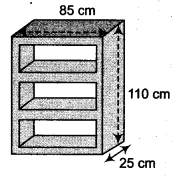
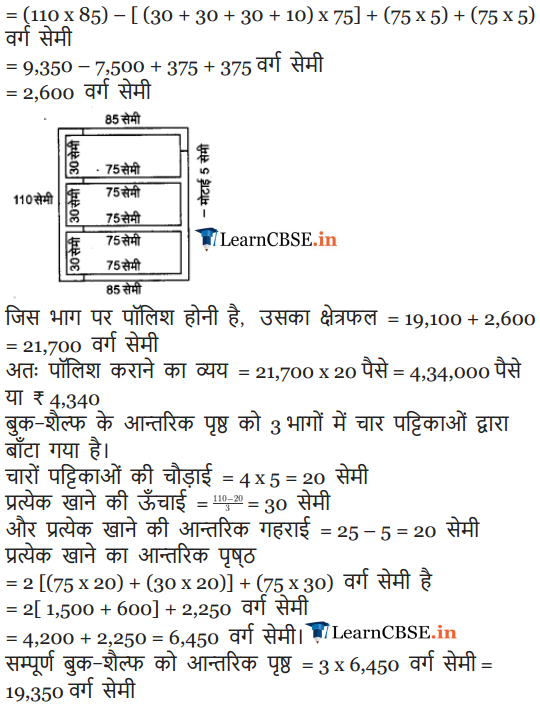
A wooden bookshelf has external dimensions as follows : Height = 110cm, Depth = 25cm, Breadth = 85cm (see figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing-is 20 paise per cm2 and the rate of pointing is 10 paise per cm2, find the total expenses required for palishing and painting the surface of the bookshelf.

Solution:
Here, l = 85 cm b = 25 cm and h = 110 cm
Area of the bookshelf of outer surface = 2 lb + 2bh + hl
= [2(85 x 25)+ 2(110 x 25)+ 85×110] cm2 = (4250 + 5500 + 9350) cm2 = 19100 cm2
Cost of polishing of the outer surface of bookshelf
= 19100 x (frac { 20 }{ 100 }) = ₹ 3820
Thickness of the plank = 5 cm
Internal height of bookshelf = (110 – 2 x 5) = 100 cm
Internal depth of bookshelf = (25 – 5) = 20 cm
Internal breadth of bookshelf = 85 – 2 x 5 = 75 cm
Hence, area of the internal surface of bookshelf
= 2(75 x 20)+ 2(100x 20)+ 75×100
= 3000 + 4000 + 7500 = 14500 cm2
So, cost of painting of internal surface of bookshelf
= 14500 x (frac { 10 }{ 100 }) = ₹1450
Hence, total costing of polishing and painting = 3820 + 1450= ₹ 5270

Ex 13.9 Class 9 Maths Question 2.
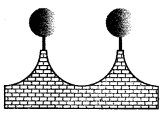
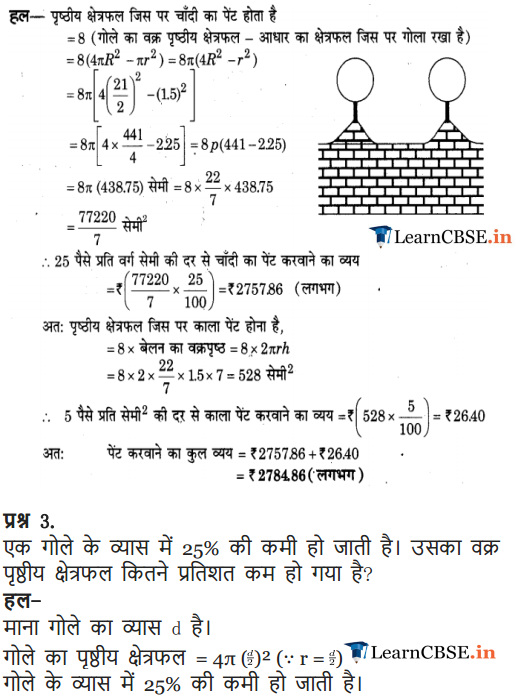
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in figure. Eight such spheres are-used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm2 and black paint costs 5 paise per cm2.

Solution:
It is obvious, we have to subtract the cost of the sphere that is resting on the supports while calculating the cost of silver paint.
Surface area to be silver paint

Ex 13.9 Class 9 Maths Question 3.
The diameter of a sphere is decreased by 25%. By what per cent does its curved surface area decrease?
Solution:
Let d be the diameter of the sphere

NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes (Hindi Medium) Ex 13.9

<!– –>