Square Roots Definition, Methods and Cube Roots List
Read the article to get detailed information about square roots, methods to find the square roots of a number, square roots and cube roots, and a list of square roots.
Square Roots: The square root of a number is multiplying factor of a number which when multiplied by itself hives the actual number. The square root is just the opposite method of squaring a number. In squaring of a number same number is multiplied by itself giving the square of a number while in square root the original number is obtained on squaring the number. The square of any number is always a positive number while the square root of a number has both positive and negative values. We can understand the square and square root easily by taking a simple example. Suppose if ‘x’ is a square of the number ‘y’ means x × x = y but if ‘x’ is a square root of ‘y’ means x2= y.
Square Roots
A Square root is a number that when multiplying gives the original number. It is like a factor, both square and square roots are a type of exponent. In other square roots can be defined as the number whose value has the power of 1/2 of a number. The symbol to represent the square root is √ which is called radical in mathematics and the number inside or called the radicand. For example, suppose a number 16 which can be obtained by multiplying 4 by 4 i.e. 4 × 4 = 16 me, and 16 is a square of 4. And suppose a number √9 on squaring the number √32 = 3 so the square root of √9 is 3. Here we will discuss the square root in detail. So refer to the below content to understand the square root in a good manner.
How to find Square Root?
The square root of a number is the square of a number that gives the original number. When finding a square root of a number firstly we need to find whether the number is a perfect square or imperfect. A perfect square is a number that can be expressed in the form of power 2. The square root of the perfect square can be found easily by factoring it into the prime factors. If a number is an imperfect square then the long division method needs to be performed on it which is discussed below in the article.
To find the square root of a number following four methods are used:
- Square Root by Prime Factorization
- Square Root by Repeated Subtraction Method
- Square Root by Long Division Method
- Square Root by Estimation Method
We will discuss all the above four methods in detail with a suitable example.
1. Square Root by Prime Factorisation Method
The square root of a perfect square number can be found easily by Prime Factorisation Method. In this method, some steps need to be followed to find the square root of a number listed below:
- Divide the given number into its prime factors.
- Form pairs of similar factors such that both factors in each pair are equal.
- Take one factor from the pair.
- Find the product of the factors obtained by taking one factor from each pair.
- The product gives the square root of the given number.
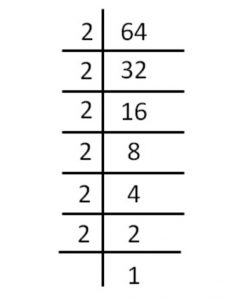
64 = 2×2×2×2×2×2×2
On pairing, we get 2×2×2 = 8
So the square root of 64 is 8.
2. Square Root by Repeated Subtraction Method
In the Repeated Subtraction Method, the square root of a number can be found by following the below steps if a given number is a perfect square.
- Repeatedly subtract the consecutive odd numbers from the given number
- Subtract till the difference remains zero
- The number of times we subtract will be the required square root
For example, let us find the square root of the number 36
- 36 – 1 = 35
- 35 – 3 = 32
- 32 – 5 = 27
- 27 – 7 = 20
- 20 – 9 = 11
- 11 – 11 = 0
Since, the subtraction is done 6 times, hence the square root of 36 is 6
3. Square Root by Long Division Method
Using the long division method the square roots of imperfect squares can be found easily. The method can be understood by the below steps.
- Place a bar over every pair of digits of the number starting from the units’ place (right-side).
- Then we divide the left-most number by the largest number whose square is less than or equal to the number in the left-most pair.
Calculate the square root of 17.64

The square root of 17.64 by the long division method is found to be 4.2
4. Square Root by Estimation Method
This method used approximation to find the square root of a number. The square root can be found by guessing the approximate value.
For example, we know that the square root of 4 is 2 and the square root of 9 is 3, thus we can guess, that the square root of 5 will lie between 2 and 3.
But, we need to check the value of √5 is nearer to 2 or 3. Let us find the squares 2.2 and 2.8.
- 2.22 = 4.84
- 2.82 = 7.84
Since the square of 2.2 gives 5 approximately, thus we can estimate the square root of 5 is equal to 2.2 approximately.
Square Root 4
The square root of 4 is denoted by √4. We know that 4 is a perfect square whose square root can be found easily by the prime factorization method or repeated subtraction method. The square root of 4 is 2. But the square roots have two values always positive and negative as we already discussed. So √4 has two values +2 and -2.
Square roots 1 to 30
As we discussed the square riots can be found easily using the four methods mentioned above. The list of square roots from 1 to 30 is mentioned here.
| Square Roots 1 to 30 | ||
| √1 | = | 1 |
| √2 | = | 1.4142 |
| √3 | = | 1.732 |
| √4 | = | 2 |
| √5 | = | 2.236 |
| √6 | = | 2.4494 |
| √7 | = | 2.6457 |
| √8 | = | 2.8284 |
| √9 | = | 3 |
| √10 | = | 3.1622 |
| √11 | = | 3.3166 |
| √12 | = | 3.4641 |
| √13 | = | 3.6055 |
| √14 | = | 3.7416 |
| √15 | = | 3.8729 |
| √16 | = | 4 |
| √17 | = | 4.1231 |
| √18 | = | 4.2426 |
| √19 | = | 4.3588 |
| √20 | = | 4.4721 |
| √21 | = | 4.5825 |
| √22 | = | 4.6904 |
| √23 | = | 4.7958 |
| √24 | = | 4.8989 |
| √25 | = | 5 |
| √26 | = | 5.099 |
| √27 | = | 5.1961 |
| √28 | = | 5.2915 |
| √29 | = | 5.3851 |
| √30 | = | 5.4772 |
Square Roots and Squares
The square root is a factor multiplying with a given number that gives the original number while the square is a number that is multiplied by itself. Both roots and squares are considered exponents. They are both opposite to each other. The examples of both square and square roots are discussed above already.
Square Roots and Cube Roots
To find the square root of any number, we need to find a number that when multiplied twice by itself gives the original number. Similarly, to find the cube root of any number we need to find a number that when multiplied three times by itself gives the original number.
Notation: The square root is denoted by the symbol ‘√’, whereas the cube root is denoted by ‘∛’.
Examples:
- √4 = √(2 × 2) = 2
- ∛27 = ∛(3 × 3 × 3) = 3
Square Roots and Cube Roots List
The list of square roots is discussed below which will be helpful for the students to make their preparation boost for upcoming exams. So refer to the list below for the same.
| Number x |
Square x2 |
Cube x3 |
Square Root x1/2 |
Cubic Root x1/3 |
|---|---|---|---|---|
| 1 | 1 | 1 | 1.000 | 1.000 |
| 2 | 4 | 8 | 1.414 | 1.260 |
| 3 | 9 | 27 | 1.732 | 1.442 |
| 4 | 16 | 64 | 2.000 | 1.587 |
| 5 | 25 | 125 | 2.236 | 1.710 |
| 6 | 36 | 216 | 2.449 | 1.817 |
| 7 | 49 | 343 | 2.646 | 1.913 |
| 8 | 64 | 512 | 2.828 | 2.000 |
| 9 | 81 | 729 | 3.000 | 2.080 |
| 10 | 100 | 1000 | 3.162 | 2.154 |
| 11 | 121 | 1331 | 3.317 | 2.224 |
| 12 | 144 | 1728 | 3.464 | 2.289 |
| 13 | 169 | 2197 | 3.606 | 2.351 |
| 14 | 196 | 2744 | 3.742 | 2.410 |
| 15 | 225 | 3375 | 3.873 | 2.466 |
| 16 | 256 | 4096 | 4.000 | 2.520 |
| 17 | 289 | 4913 | 4.123 | 2.571 |
| 18 | 324 | 5832 | 4.243 | 2.621 |
| 19 | 361 | 6859 | 4.359 | 2.668 |
| 20 | 400 | 8000 | 4.472 | 2.714 |
| 21 | 441 | 9261 | 4.583 | 2.759 |
| 22 | 484 | 10648 | 4.690 | 2.802 |
| 23 | 529 | 12167 | 4.796 | 2.844 |
| 24 | 576 | 13824 | 4.899 | 2.884 |
| 25 | 625 | 15625 | 5.000 | 2.924 |
| 26 | 676 | 17576 | 5.099 | 2.962 |
| 27 | 729 | 19683 | 5.196 | 3.000 |
| 28 | 784 | 21952 | 5.292 | 3.037 |
| 29 | 841 | 24389 | 5.385 | 3.072 |
| 30 | 900 | 27000 | 5.477 | 3.107 |
| 31 | 961 | 29791 | 5.568 | 3.141 |
| 32 | 1024 | 32768 | 5.657 | 3.175 |
| 33 | 1089 | 35937 | 5.745 | 3.208 |
| 34 | 1156 | 39304 | 5.831 | 3.240 |
| 35 | 1225 | 42875 | 5.916 | 3.271 |
| 36 | 1296 | 46656 | 6.000 | 3.302 |
| 37 | 1369 | 50653 | 6.083 | 3.332 |
| 38 | 1444 | 54872 | 6.164 | 3.362 |
| 39 | 1521 | 59319 | 6.245 | 3.391 |
| 40 | 1600 | 64000 | 6.325 | 3.420 |
| 41 | 1681 | 68921 | 6.403 | 3.448 |
| 42 | 1764 | 74088 | 6.481 | 3.476 |
| 43 | 1849 | 79507 | 6.557 | 3.503 |
| 44 | 1936 | 85184 | 6.633 | 3.530 |
| 45 | 2025 | 91125 | 6.708 | 3.557 |
| 46 | 2116 | 97336 | 6.782 | 3.583 |
| 47 | 2209 | 103823 | 6.856 | 3.609 |
| 48 | 2304 | 110592 | 6.928 | 3.634 |
| 49 | 2401 | 117649 | 7.000 | 3.659 |
| 50 | 2500 | 125000 | 7.071 | 3.684 |
| 51 | 2601 | 132651 | 7.141 | 3.708 |
| 52 | 2704 | 140608 | 7.211 | 3.733 |
| 53 | 2809 | 148877 | 7.280 | 3.756 |
| 54 | 2916 | 157464 | 7.348 | 3.780 |
| 55 | 3025 | 166375 | 7.416 | 3.803 |
| 56 | 3136 | 175616 | 7.483 | 3.826 |
| 57 | 3249 | 185193 | 7.550 | 3.849 |
| 58 | 3364 | 195112 | 7.616 | 3.871 |
| 59 | 3481 | 205379 | 7.681 | 3.893 |
| 60 | 3600 | 216000 | 7.746 | 3.915 |
| 61 | 3721 | 226981 | 7.810 | 3.936 |
| 62 | 3844 | 238328 | 7.874 | 3.958 |
| 63 | 3969 | 250047 | 7.937 | 3.979 |
| 64 | 4096 | 262144 | 8.000 | 4.000 |
| 65 | 4225 | 274625 | 8.062 | 4.021 |
| 66 | 4356 | 287496 | 8.124 | 4.041 |
| 67 | 4489 | 300763 | 8.185 | 4.062 |
| 68 | 4624 | 314432 | 8.246 | 4.082 |
| 69 | 4761 | 328509 | 8.307 | 4.102 |
| 70 | 4900 | 343000 | 8.367 | 4.121 |
| 71 | 5041 | 357911 | 8.426 | 4.141 |
| 72 | 5184 | 373248 | 8.485 | 4.160 |
| 73 | 5329 | 389017 | 8.544 | 4.179 |
| 74 | 5476 | 405224 | 8.602 | 4.198 |
| 75 | 5625 | 421875 | 8.660 | 4.217 |
| 76 | 5776 | 438976 | 8.718 | 4.236 |
| 77 | 5929 | 456533 | 8.775 | 4.254 |
| 78 | 6084 | 474552 | 8.832 | 4.273 |
| 79 | 6241 | 493039 | 8.888 | 4.291 |
| 80 | 6400 | 512000 | 8.944 | 4.309 |
| 81 | 6561 | 531441 | 9.000 | 4.327 |
| 82 | 6724 | 551368 | 9.055 | 4.344 |
| 83 | 6889 | 571787 | 9.110 | 4.362 |
| 84 | 7056 | 592704 | 9.165 | 4.380 |
| 85 | 7225 | 614125 | 9.220 | 4.397 |
| 86 | 7396 | 636056 | 9.274 | 4.414 |
| 87 | 7569 | 658503 | 9.327 | 4.431 |
| 88 | 7744 | 681472 | 9.381 | 4.448 |
| 89 | 7921 | 704969 | 9.434 | 4.465 |
| 90 | 8100 | 729000 | 9.487 | 4.481 |
| 91 | 8281 | 753571 | 9.539 | 4.498 |
| 92 | 8464 | 778688 | 9.592 | 4.514 |
| 93 | 8649 | 804357 | 9.644 | 4.531 |
| 94 | 8836 | 830584 | 9.695 | 4.547 |
| 95 | 9025 | 857375 | 9.747 | 4.563 |
| 96 | 9216 | 884736 | 9.798 | 4.579 |
| 97 | 9409 | 912673 | 9.849 | 4.595 |
| 98 | 9604 | 941192 | 9.899 | 4.610 |
| 99 | 9801 | 970299 | 9.950 | 4.626 |
| 100 | 10000 | 1000000 | 10.000 | 4.642 |
Square Roots: FAQs
Que.1 What are squares?
Ans – The squares are a twice multiplication of the number itself. For example, 25 is a square of 5 i.e. 5×5 = 25
Que.2 What are square roots?
Ans – Square root is just opposite to square. Is the 1/2 power of a number. For example, the square root of 9 is 3 i.e. √9 = 3
Que.1 What are squares?
Ans – The squares are a twice multiplication of the number itself. For example, 25 is a square of 5 i.e. 5×5 = 25
Que.2 What are square roots?
Ans – Square root is just opposite to square. Is the 1/2 power of a number. For example, the square root of 9 is 3 i.e. √9 = 3
Comments are closed