NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.2
NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.2
Ex 9.2 Class 8 Maths Question 1.
Find the product of the following pairs of monomials.
(i) 4, 7p
(ii) -4p, 7p
(iii) -4p, 7pq
(iv) 4p3, -3p
(v) 4p, 0
Solution:
(i) 4 × 7p = (4 × 7) × p = 28p
(ii) -4p × 7p = (-4 × 7) × p × p = -28p2
(iii) -4p × 7pq = (-4 × 7) × p × pq = -28p2q
(iv) 4p3 × -3p = (4 × -3) × p3 × p = -12p4
(v) 4p x 0 = (4 × 0) × p = 0 × p = 0
Ex 9.2 Class 8 Maths Question 2.
Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively.
(p, q); (10m, 5n); (20×2, 5y2); (4x, 3×2); (3mn, 4np)
Solution:
(i) Length = p units and breadth = q units
Area of the rectangle = length × breadth = p × q = pq sq units
(ii) Length = 10 m units, breadth = 5n units
Area of the rectangle = length × breadth = 10 m × 5 n = (10 × 5) × m × n = 50 mn sq units
(iii) Length = 20×2 units, breadth = 5y2 units
Area of the rectangle = length × breadth = 20×2 × 5y2 = (20 × 5) × x2 × y2 = 100x2y2 sq units
(iv) Length = 4x units, breadth = 3×2 units
Area of the rectangle = length × breadth = 4x × 3×2 = (4 × 3) × x × x2 = 12×3 sq units
(v) Length = 3mn units, breadth = 4np units
Area of the rectangle = length × breadth = 3mn × 4np = (3 × 4) × mn × np = 12mn2p sq units
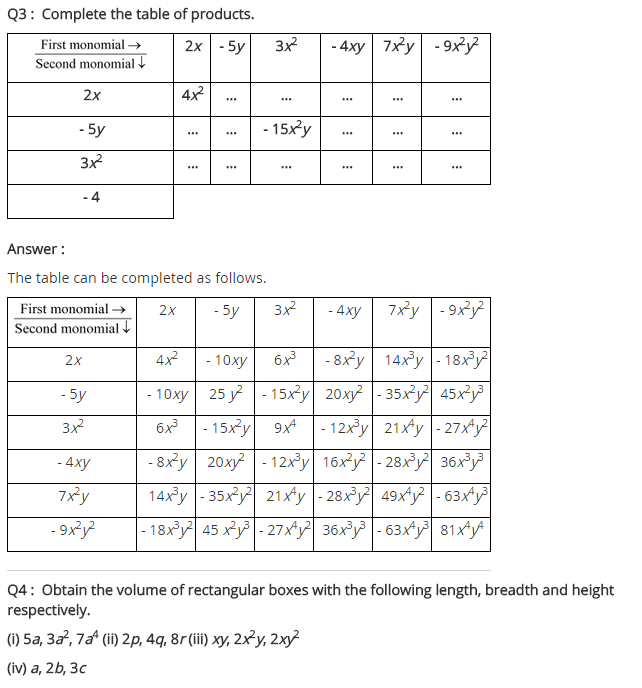
Ex 9.2 Class 8 Maths Question 3.
Complete the table of Products.
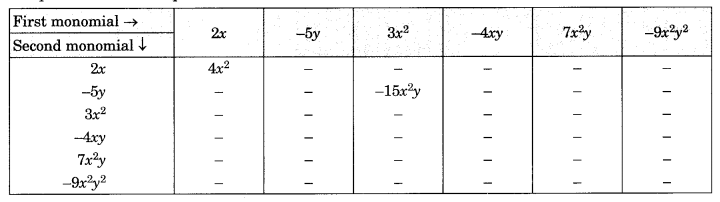
Solution:
Completed Table
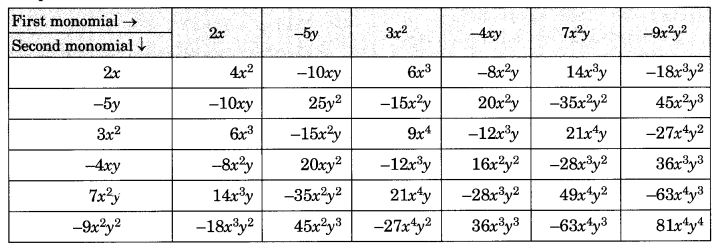
Ex 9.2 Class 8 Maths Question 4.
Obtain the volume of rectangular boxes with the following length, breadth and height respectively.
(i) 5a, 3a2, 7a4
(ii) 2p, 4q, 8r
(iii) xy, 2x2y, 2xy2
(iv) a, 2b, 3c
Solution:
(i) Here, length = 5a, breadth = 3a2, height = 7a4
Volume of the box = l × b × h = 5a × 3a2 × 7a4 = 105 a7 cu. units
(ii) Here, length = 2p, breadth = 4q, height = 8r
Volume of the box = l × b × h = 2p × 4q × 8r = 64pqr cu. units
(iii) Here, length = xy, breadth = 2x2y, height = 2xy2
Volume of the box = l × b × h = xy × 2x2y × 2xy2 = (1 × 2 × 2) × xy × x2y × xy2 = 4x4y4 cu. units
(iv) Here, length = a, breadth = 2b, height = 3c
Volume of the box = length × breadth × height = a × 2b × 3c = (1 × 2 × 3)abc = 6 abc cu. units
Ex 9.2 Class 8 Maths Question 5.
Obtain the product of
(i) xy, yz, zx
(ii) a, -a2, a3
(iii) 2, 4y, 8y2, 16y3
(iv) a, 2b, 3c, 6abc
(v) m, -mn, mnp
Solution:
(i) xy × yz × zx = x2y2z2
(ii) a × (-a2) × a3 = -a6
(iii) 2 × 4y × 8y2 × 16y3 = (2 × 4 × 8 × 16) × y × y2 × y3 = 1024y6
(iv) a × 2b × 3c × 6abc = (1 × 2 × 3 × 6) × a × b × c × abc = 36 a2b2c2
(v) m × (-mn) × mnp = [1 × (-1) × 1 ]m × mn × mnp = -m3n2p


<!– –>
Comments are closed