NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities
NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.1
Ex 9.1 Class 8 Maths Question 1.
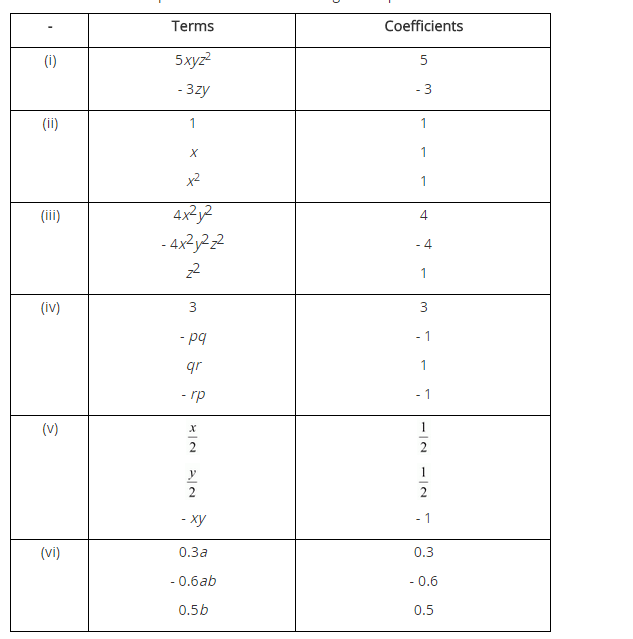
Identify the terms, their coefficients for each of the following expressions.
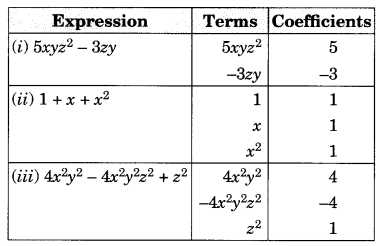
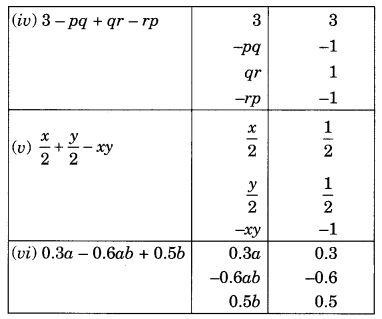
(i) 5xyz2 – 3zy
(ii) 1 + x + x2
(iii) 4x2y2 – 4x2y2z2 + z2
(iv) 3 – pq + qr – rp
(v) (frac { x }{ 2 }) + (frac { y }{ 2 }) – xy
(vi) 0.3a – 0.6ab + 0.5b
Solution:
Ex 9.1 Class 8 Maths Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?
x + y, 1000, x + x2 + x3 + x4, 7 + y + 5x, 2y – 3y2, 2y – 3y2 + 4y3, 5x – 4y + 3xy, 4z – 15z2, ab + bc + cd + da, pqr, p2q + pq2, 2p + 2q
Solution:

Ex 9.1 Class 8 Maths Question 3.
Add the following:
(i) ab – bc, bc – ca, ca – ab
(ii) a – b + ab, b – c + bc, c – a + ac
(iii) 2p2q2 – 3pq + 4, 5 + 7pq – 3p2q2
(iv) l2 + m2, m2 + n2, n2 + l2, 2lm + 2mn + 2nl
Solution:
(i) Given: ab – bc, bc – ca, ca – ab
We have
(ab – bc) + (bc – ca) + (ca – ab) (Adding all the terms)
= ab – bc + bc – ca + ca – ab
= (ab – ab) + (bc – bc) + (ca – ca) (Collecting the like terms together)
= 0 + 0 + 0
= 0
(ii) Given:
a – b + ab, b – c + bc, c – a + ac
We have (a – b + ab) + (b – c + bc) + (c – a + ac) (Adding all the terms)
= a – b + ab + b – c + bc + c – a + ac
= (a – a) + (b – b) + (c – c) + ab + bc + ac (Collecting all the like terms together)
= 0 + 0 + 0 + ab + bc + ac
= ab + bc + ac
(iii) Given:
2p2q2 – 3pq + 4, 5 + 7pq – 3p2q2
By arranging the like terms in the same column, we have
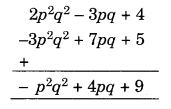
(Adding columnwise)
(iv) Given: l2 + m2, m2 + n2, n2 + l2, 2lm + 2mn + nl
By arranging the like terms in the same column, we have

Thus, the sum of the given expressions is 2(l2 + m2 + n2 + lm + mn + nl)
Ex 9.1 Class 8 Maths Question 4.
(a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
(6) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract 4p2q – 3pq + 5pq2 – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq2 + 5p2q
Solution:
(a) Arranging the like terms column-wise, we have
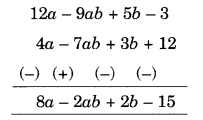
[Change the signs of all the terms of lower expressions and then add]
(b) Arranging the like terms column-wise, we have
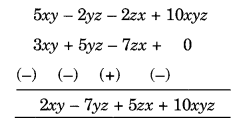
[Change the signs of all the terms of lower expressions and then add]
(c) Arranging the like terms column-wise, we have
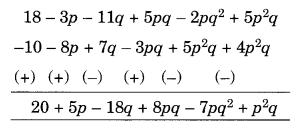
[Change the signs of all the terms of lower expressions and then add]
The terms are p2q – 7pq2 + 8pq – 18q + 5p + 20



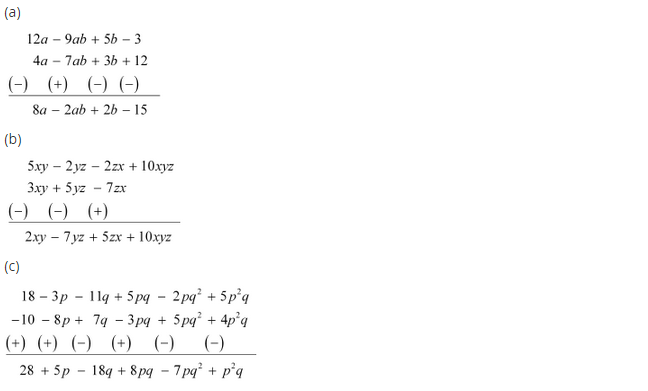
<!– –>
Comments are closed